Question

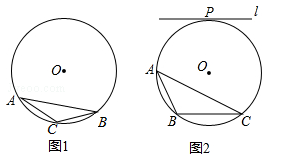
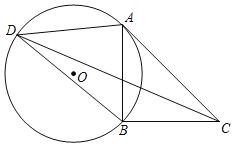
【题目】如图，线段AB为⊙O的一条弦，以AB为直角边作等腰直角△ABC，直线AC恰好是⊙O的切线，点D为⊙O上的一点，连接DA，DB，DC，若DA＝3，DB＝4，则DC的长为_____．

Answer 1

【答案】．

【解析】

延长CB交⊙O于F，连接AF，作BE⊥DB交DF的延长线于E，连接AE，如图，先利用∠ABF＝90°得到AF为⊙O的直径，再根据切线的性质得到∠FAC＝90°，则∠BAF＝∠AFB＝45°，接着判断△BDE为等腰直角三角形得到BD＝BE，DE＝BD＝4，再证明△ABE≌△CBD得到AE＝CD，然后利用勾股定理计算出AE即可CD的长．

解：延长CB交⊙O于F，连接AF，作BE⊥DB交DF的延长线于E，连接AE，如图，

∵△ABC为等腰直角三角形，

∴BA＝BC，∠BAC＝45°，∠ABC＝90°，

∴∠ABF＝90°，

∴AF为⊙O的直径，

∵直线AC是⊙O的切线，

∴AF⊥AC，

∴∠FAC＝90°，

∴∠BAF＝∠AFB＝45°，

∴∠BDF＝∠BAF＝45°，

∴△BDE为等腰直角三角形，

∴BD＝BE，DE＝BD＝4

∵∠ABE＝∠DBE+∠ABD＝90°+∠ABD，∠CBD＝∠ABC+∠ABD＝90°+∠ABD，

∴∠ABE＝∠CBD，

而BA＝BC，BD＝BE，

∴△ABE≌△CBD（SAS），

∴AE＝CD，

∵AF为直径，

∴∠ADF＝90°，

在Rt△ADE中，AE＝＝，

∴CD＝．

故答案为．