Question

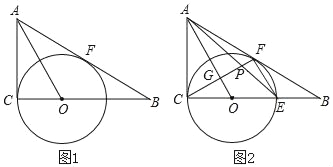
【题目】如图，△ABC中，∠ACB=90°，点E在BC上，以CE为直径的⊙O交AB于点F，AO∥EF

（1）求证：AB是⊙O的切线；

（2）如图2，连结CF交AO于点G，交AE于点P，若BE=2，BF=4，求的值．

Answer 1

【答案】（1）证明见解析（2）2

【解析】

（1）连接OF，如图1，证明△AOC≌△AOF，根据全等三角形的性质可得∠AFO=∠ACO=90°，即可证得AB是⊙O的切线；

（2）如图2，在Rt△OFB中，设OE=OF=r，利用勾股定理求得r=3，从而得OB=5，设AC=AF=t，则AB=4+t，在Rt△ACB中，利用勾股定理求得t，即可得AC=6，从而可得AO长，然后证明△ACO∽△AGO，继而可推导得出AO=AG，再证明△BEF∽△BOA，从而可推导得出，再证明△PEF∽△PAG，根据相似三角形的性质即可求得=2．

（1）连接OF，如图1，

∵OA∥EF，

∴∠1=∠3，∠2=∠4，

∵OE=OF，

∴∠3=∠4，

∴∠1=∠2，

在△AOC和△AOF中，

，

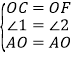∴△AOC≌△AOF，

∴∠ACO=∠AFO=90°，

∴OF⊥AB，

∴AB是⊙O的切线；

（2）如图2，在Rt△OFB中，设OE=OF=r，

∵OF2+BF2=OB2，

∴r2+42=（r+2）2，解得r=3，

∴OB=5，

设AC=AF=t，则AB=4+t，

在Rt△ACB中，t2+82=（t+4）2，解得t=6，

即AC=6，

∴AO=，

∵∠CAO=∠GAO，∠ACO=∠AGC=90°，

∴△ACO∽△AGO，

∴AC：AO=AG：AC，

∴AC2=AOAG，

∴AG=，

∴AO=AG，

∵OA∥EF，

∴△BEF∽△BOA，

∴，

∴，

∴，

∵EF∥GA，

∴△PEF∽△PAG，

∴=2．