题目内容
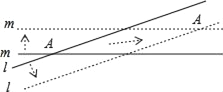
【题目】将![]() 沿直线
沿直线![]() 平移到
平移到![]() 的位置,连接
的位置,连接![]() 、
、![]() .
.
(1)如图1,写出线段![]() 与
与![]() 的关系__________;
的关系__________;
(2)如图1,求证:![]() ;
;

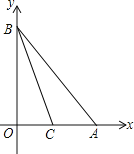
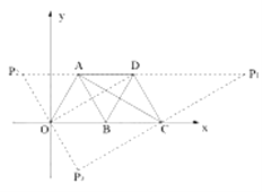
(3)如图2,当![]() 是边长为2的等边三角形时,以点
是边长为2的等边三角形时,以点![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系.求出点
轴建立平面直角坐标系.求出点![]() 的坐标,使得以
的坐标,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.

【答案】(1)![]() 且
且![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)根据平行四边形的判定与性质即可求解;
(2)过![]() 作
作![]() ,设
,设![]() ,
,![]() ,根据勾股定理与平行四边形的性质即可求解;(3)先根据等边三角形的性质求出
,根据勾股定理与平行四边形的性质即可求解;(3)先根据等边三角形的性质求出![]() ,
,![]() ,
,![]() ,根据平行四边形的性质求出
,根据平行四边形的性质求出![]() ,
,![]() ,再分以
,再分以![]() 为对角线时的一种情况, ②以
为对角线时的一种情况, ②以![]() 为边时的两种情况分别进行讨论求解.
为边时的两种情况分别进行讨论求解.
(1)∵将![]() 沿直线
沿直线![]() 平移到
平移到![]() 的位置,
的位置,
∴AO∥DB,AO=DB,
故答案为:AO∥DB且AO=DB,
(2)解:
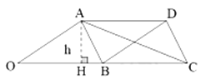
过![]() 作
作![]() ,设
,设![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]()
![]()
∵![]()
∴![]()
∵![]()
∴![]()
∵![]() 且
且![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]() ,
,![]()
∴![]()
(3)解:如图所示,满足题意的![]() 点坐标有3个。
点坐标有3个。
∵等边![]() 的边长为2
的边长为2
∴![]() ,
,![]() ,
,![]()
∵![]() ,
,![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]()
∴![]()
∵![]() ∴
∴![]()
①以![]() 为对角线时,四边形
为对角线时,四边形![]() 为平行四边形
为平行四边形
∴![]() ,
,![]()
∴![]() .
.
②以![]() 为边时,有两种情况:
为边时,有两种情况:
当四边形![]() 为平行四边形时,
为平行四边形时,
![]()
∴![]() .
.
当四边形![]() 为平行四边形时,
为平行四边形时,
![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]() .
.
综上所述,满足题意的![]() 坐标有:
坐标有:![]() ,
,![]() ,
,![]() .
.

【题目】![]() 市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
市首批一次性投放公共自行车700辆供市民租用出行,由于投入数量不够, 导致出现需要租用却未租到车的现象,现随机抽取的某五天在同一时段的调查数据汇成如下表格.
请回答下列问题:
时间 | 第一天7:00﹣8:00 | 第二天7:00﹣8:00 | 第三天7:00﹣8:00 | 第四天7:00﹣8:00 | 第五天7:00﹣8:00 |
需要租用自行车却未租到车的人数(人) | 1500 | 1200 | 1300 | 1300 | 1200 |
(1)表格中的五个数据(人数)的中位数是多少?
(2)由随机抽样估计,平均每天在7:00-8:00 :需要租用公共自行车的人数是多少?