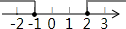题目内容
16.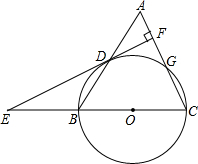 如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,已知等腰△ABC,AC=BC=10.AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.(1)求证:直线EF是⊙O的切线;
(2)求DF的长.
分析 (1)求证直线EF是⊙O的切线,只要连接OD证明OD⊥EF即可;
(2)由BC是⊙O直径,得到CD⊥AB,在Rt△ACD中,由勾股定理得:CD=$\sqrt{{10}^{2}{-6}^{2}}$=8,由于EF⊥AC,CD⊥AB,得出∠AFD=∠CDB=90°,推出△ADF∽△BCD,得到比例式,即可得到结论.
解答  (1)证明:连接CD,OD,
(1)证明:连接CD,OD,
∵AC=BC,
∴∠A=∠ABC,
∵OD=OB,
∴∠ABC=∠BDO,
∴∠A=∠BDO,
∴OD∥AC,
∵EF⊥AC,
∴EF⊥OD,
∵OD为半径,
∴EF是⊙O的切线;
(2)解:∵BC是⊙O直径,
∴CD⊥AB,
∵AC=BC=10,又AB=12,
∴AD=BD=6,
在Rt△ACD中,由勾股定理得:CD=$\sqrt{{10}^{2}{-6}^{2}}$=8,
∵EF⊥AC,CD⊥AB,
∴∠AFD=∠CDB=90°,
又∵∠A=∠CBD,
∴△ADF∽△BCD,
∴$\frac{AD}{BC}=\frac{DF}{CD}$,
∴$\frac{6}{10}=\frac{DF}{8}$,即DF=$\frac{24}{5}$.
点评 本题主要考查了相似三角形的判定与性质、圆周角定理、切线的判定、余角的概念与性质、等腰三角形的性质及平行线的性质等知识点,关键在于运用数形结合的思想,结合相关性质定理,正确的做出辅助线是解题的关键.

练习册系列答案
相关题目
20. 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
 如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )
如图,在△ABC中,AB=AC,DE∥BC,则下列结论中不正确的是( )| A. | AD=AE | B. | DB=EC | C. | ∠ADE=∠C | D. | DE=$\frac{1}{2}$BC |
7.不等式组$\left\{\begin{array}{l}{2x-1<5}\\{x-2>-3}\end{array}\right.$的解集是( )
| A. | 1<x<6 | B. | -1<x<3 | C. | 1<x<3 | D. | -1<x<6 |