题目内容
 如图所示,已知等腰直角△ABC中,∠ACB=90°,AC=BC,AF是∠BAC的平分线,交BC于点E,BF⊥AF于点F,求证:AE=2BF.
如图所示,已知等腰直角△ABC中,∠ACB=90°,AC=BC,AF是∠BAC的平分线,交BC于点E,BF⊥AF于点F,求证:AE=2BF.考点:全等三角形的判定与性质
专题:证明题
分析:延长线段BF与AC的延长线交于点M.根据角平分线的性质,等腰直角三角形的性质,由AAS证明△ACE≌△BCM,再根据全等三角形的性质即可求解.
解答: 解:延长线段BF与AC的延长线交于点M.
解:延长线段BF与AC的延长线交于点M.
∵AF为∠BAC的平分线,BF⊥AF,
∴AM=AB,
∵∠ACB=90°,
∴∠CAB=45°,
∵AE为△ABC的角平分线,
∴∠AEC=90°-∠CAE=90°-22.5°=67.5°,
∴∠M=∠AEC=67.5°,
在△ACE与△BCM中,
,
∴△ACE≌△BCM(AAS),
∴AE=BM=2BF.
 解:延长线段BF与AC的延长线交于点M.
解:延长线段BF与AC的延长线交于点M.∵AF为∠BAC的平分线,BF⊥AF,
∴AM=AB,
∵∠ACB=90°,
∴∠CAB=45°,
∵AE为△ABC的角平分线,
∴∠AEC=90°-∠CAE=90°-22.5°=67.5°,
∴∠M=∠AEC=67.5°,
在△ACE与△BCM中,
|
∴△ACE≌△BCM(AAS),
∴AE=BM=2BF.
点评:此题考查学生灵活运用全等三角形的判定与性质解决数学问题,是一道综合题.关键是作出辅助线构造全等三角形.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
某商店出售两件上衣,每件按60元出售,这样一件赚了25%,另一件赔了25%,那么这两件大衣出售后,商店的赚和赔的情况是( )
| A、不赔不赚 | B、赔了8元 |
| C、赚了8元 | D、赔了15元 |
过A、B、C三点,最多可确定直线的条数是( )
| A、1条 | B、3条 |
| C、1条或2条 | D、1条或3条 |
以下几种图形:①三角形 ②正方体 ③圆 ④圆锥 ⑤圆柱 ⑥正方形 ⑦梯形 ⑧球⑨等腰三角形,其中不属于平面图形的是( )
| A、②③④⑧ | B、②④⑤ |
| C、④⑤⑧⑨ | D、②④⑤⑧ |
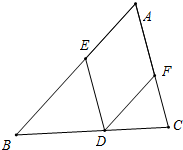 菱形AEDF内接于△ABC,且AB=21cm,AC=15cm,BC=18cm,求BD,CD及菱形的边长.
菱形AEDF内接于△ABC,且AB=21cm,AC=15cm,BC=18cm,求BD,CD及菱形的边长. 如图,在四边形ABEC中,对角线BC,AE交于点D,已知AC=AB,CE=BE,试说明AE垂直平分BC.
如图,在四边形ABEC中,对角线BC,AE交于点D,已知AC=AB,CE=BE,试说明AE垂直平分BC.