题目内容
(1)化简并求值: ,其中y满足y2+2y-1=0.
,其中y满足y2+2y-1=0.
(2)已知 ,化简求值:
,化简求值: .
.
(3)计算:
(4)解分式方程: =1.
=1.
解:(1)原式=( -
- )÷
)÷
= ÷
÷
=
由y2+2y-1=0得y2+2y=1.
∴原式=1;
(2)原式= -
-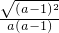 -
- =a-1,
=a-1,
当 时,原式=
时,原式=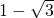 ;
;
(3)原式=5 -(2
-(2 +
+ )+3-
)+3-
=5 -2
-2 -
- +3-
+3-
= ;
;
(4)原方程可化为: +
+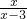 +
+ =1,
=1,
 +
+ +
+ =1
=1
 =1
=1
解得:x=- ,
,
检验:把x=- 代入(x-1)(x-3)≠0,
代入(x-1)(x-3)≠0,
∴原方程的解为x=- .
.
分析:(1)(2)先把原式化简,化为最简后再代数求值即可;
(3)先把各分式化简,化为最简后再按照从左到右的顺序依次计算即可.
(4)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
点评:本题考查了分式的化简求值、二次根式的化简求值以及解分式方程,此题综合性较强,计算是比较繁琐,一定要细心才行.
 -
- )÷
)÷
=
 ÷
÷
=

由y2+2y-1=0得y2+2y=1.
∴原式=1;
(2)原式=
 -
-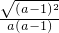 -
- =a-1,
=a-1,当
 时,原式=
时,原式=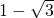 ;
;(3)原式=5
 -(2
-(2 +
+ )+3-
)+3-
=5
 -2
-2 -
- +3-
+3-
=
 ;
;(4)原方程可化为:
 +
+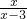 +
+ =1,
=1, +
+ +
+ =1
=1 =1
=1解得:x=-
 ,
,检验:把x=-
 代入(x-1)(x-3)≠0,
代入(x-1)(x-3)≠0,∴原方程的解为x=-
 .
.分析:(1)(2)先把原式化简,化为最简后再代数求值即可;
(3)先把各分式化简,化为最简后再按照从左到右的顺序依次计算即可.
(4)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
点评:本题考查了分式的化简求值、二次根式的化简求值以及解分式方程,此题综合性较强,计算是比较繁琐,一定要细心才行.

练习册系列答案
相关题目