题目内容
在平面直角坐标系![]() O
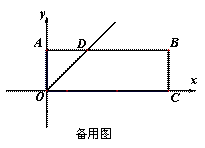
O![]() 中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒
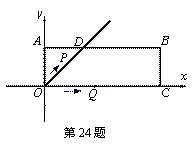
中,过原点O及点A(0,2) 、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
(1)当点P移动到点D时,求出此时t的值;
(2)当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为![]() (
(![]() ).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
 |
解:(1)∵矩形OABC, ∴∠AOC=∠OAB=90°
∵OD平分∠AOC ∴∠AOD=∠DOQ=45°……………………………………1分
∴在Rt△AOD中,∠ADO=45° ∴AO=AD=2, OD=![]() ……2分
……2分
 ∴
∴![]() ……………………………3分
……………………………3分
(2)要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°.
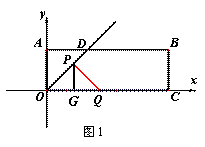
解法1:如图1,作PG⊥OC于点G,在Rt△POG中,
∵∠POQ =45°,∴ ∠OPG =45° ∵OP=![]() ,∴OG=PG=t,
,∴OG=PG=t,
∴点P(t,,t)
又∵Q(2t,0),B(6,2),根据勾股定理可得:
![]() ,
,![]() ,
,![]() ………4分
………4分
①若∠PQB=90°,则有![]() ,
,
即:![]() ,
,
整理得:![]() ,解得
,解得![]() (舍去),
(舍去),![]()
∴![]() ………6分
………6分
②若∠PBQ=90°,则有![]() ,
,
∴![]() ,
,
整理得![]() ,解得
,解得![]() .
.
 ∴当t=2或
∴当t=2或![]() 或
或![]() 时,△PQB为直角三角形. .… 8分
时,△PQB为直角三角形. .… 8分
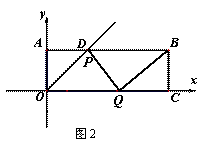
解法2:①如图2,当∠PQB=90°时,
易知∠OPQ=90°,∴BQ∥OD ∴∠BQC=∠POQ=45°
可得QC=BC=2 ∴OQ=4 ∴2t=4 ∴t=2 ……………5分
②如图3,当∠PBQ=90°时,若点Q在OC上,
作PN⊥x轴于点N,交AB于点M,
则易证∠PBM=∠CBQ∴△PMB∽△QCB
∴![]() ,∴
,∴![]() ,∴
,∴![]() , 化简得
, 化简得![]() ,
,
解得![]() ……… 6分
……… 6分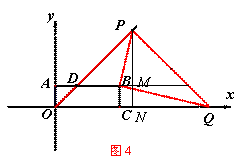 ∴
∴![]() ………………… 7分
………………… 7分
③如图4,当∠PBQ=90°时,若点Q在OC的延长线上,
作PN⊥x轴于点N,交AB延长线于点M,
则易证∠BPM=∠MBQ=∠BQC ∴△PMB∽△QCB
∴![]() ,∴
,∴![]() ,
,
∴![]() ,化简得
,化简得![]() ,
,
解得![]() ∴
∴![]() ……………… 8分
……………… 8分
(3)存在这样的t值,理由如下:将△PQB绕某点旋转180°,三个对应顶点恰好都落在抛物线上,则旋转中心为PQ中点,此时四边形![]() 为平行四边形. ………………9分
为平行四边形. ………………9分
∵PO=PQ ,由P(t,t),Q(2t,0),知旋转中心坐标可表示为(![]() )………………10分
)………………10分
∵点B坐标为(6,2), ∴点![]() 的坐标为(3t-6,t-2), .………………11分
的坐标为(3t-6,t-2), .………………11分
代入![]()
![]() ,得:
,得: ![]() ,解得
,解得![]() ……12分
……12分
(另解:第二种情况也可以直接由下面方法求解:当点P与点D重合时,PB=4,OQ=4,又PB ∥OQ,∴四边形![]() 为平行四边形,此时绕PQ中点旋转180°,点B的对应点恰好落在O处,点
为平行四边形,此时绕PQ中点旋转180°,点B的对应点恰好落在O处,点![]() 即点O.由(1)知,此时t=2. (说明:解得此t值,可得2分.)
即点O.由(1)知,此时t=2. (说明:解得此t值,可得2分.)

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案 如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4),连接OA,若在直线a上存在点P,使△AOP是等腰三角形,那么所有满足条件的点P的坐标是( )
如图,在平面直角坐标系xOy中,分别平行x、y轴的两直线a、b相交于点A(3,4),连接OA,若在直线a上存在点P,使△AOP是等腰三角形,那么所有满足条件的点P的坐标是( )