题目内容
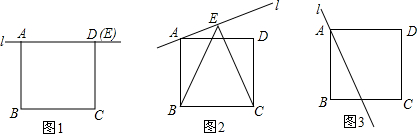
 已知⊙O过正方形ABCD顶点A、B,且与CD相切,若正方形边长为2,则圆的半径为
已知⊙O过正方形ABCD顶点A、B,且与CD相切,若正方形边长为2,则圆的半径为分析:连接OE、OB,延长EO交AB于F,设⊙O的半径为R,则OF=2-R,再由勾股定理即可求出R的值.
解答: 解:连接OE、OB,延长EO交AB于F;
解:连接OE、OB,延长EO交AB于F;
∴E是切点,
∴OE⊥CD,
∴OF⊥AB,OE=OB;
设OB=R,则OF=2-R,
在Rt△OBF中,BF=
AB=
×2=1,OB=R,OF=2-R,
∴R2=(2-R)2+12,解得R=
.
 解:连接OE、OB,延长EO交AB于F;
解:连接OE、OB,延长EO交AB于F;∴E是切点,
∴OE⊥CD,
∴OF⊥AB,OE=OB;
设OB=R,则OF=2-R,
在Rt△OBF中,BF=
| 1 |
| 2 |
| 1 |
| 2 |
∴R2=(2-R)2+12,解得R=
| 5 |
| 4 |
点评:本题涉及到正方形、圆及直角三角形的性质,涉及面较广,但难度适中.根据题意作出辅助线、构造出直角三角形是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目