Question

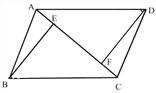
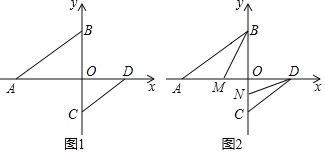
【题目】如图1，在平面直角坐标系中，点A、B、C、D均在坐标轴上，AB∥CD．

（1）求证：∠ABO+∠CDO＝90°；

（2）如图2，BM平分∠ABO交x轴于点M，DN平分∠CDO交y轴于点N，求∠BMO+∠OND的值．

Answer 1

【答案】（1）详见解析；（2）135°．

【解析】

（1）根据平行线的性质得到∠ABO＝∠DCO，然后结合等量代换证明；

（2）根据角平分线的定义、结合（1）中结论计算．

（1）证明：∵AB∥CD，

∴∠ABO＝∠DCO，

∵∠DCO+∠CDO＝90°；

∴∠ABO+∠CDO＝90°；

（2）∵BM平分∠ABO，DN平分∠CDO，

∴∠MBO＝∠ABO，∠NDO＝∠CDO，

∴∠MBO+∠NDO＝（∠ABO+∠CDO）＝45°，

∴∠BMO+∠OND＝135°．