题目内容
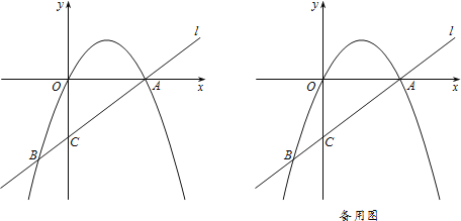
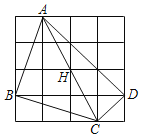
【题目】如图,在4×4的网格中,点A,B,C,D,H均在网格的格点上,下面结论:
①点H是△ABD的内心
②点H是△ABD的外心
③点H是△BCD的外心
④点H是△ADC的外心
其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
先利用勾股定理计算出AB=BC=![]() ,AD=
,AD=![]() ,CD=
,CD=![]() ,AC=
,AC=![]() ,再利用勾股定理的逆定理可得到∠ABC=∠ADC=90°,则CB⊥AB,CD⊥AD,根据角平分线定理的逆定理可判断点C不在∠BAD的角平分线上,则根据三角形内心的定义可对①进行判断;由于HA=HB=HC=HD=
,再利用勾股定理的逆定理可得到∠ABC=∠ADC=90°,则CB⊥AB,CD⊥AD,根据角平分线定理的逆定理可判断点C不在∠BAD的角平分线上,则根据三角形内心的定义可对①进行判断;由于HA=HB=HC=HD=![]() ,则根据三角形外心的定义可对②③④进行判断.
,则根据三角形外心的定义可对②③④进行判断.
解:∵AB=BC=![]() ,AD=
,AD=![]() ,CD=
,CD=![]() ,AC=
,AC=![]() ,
,
∴AB2+BC2=AC2,CD2+AD2=AC2,
∴△ABC和△ADC都为直角三角形,∠ABC=∠ADC=90°,
∵CB⊥AB,CD⊥AD,而CB≠CD,
∴点C不在∠BAD的角平分线上,
∴点H不是△ABD的内心,所以①错误;
∵HA=HB=HC=HD=![]() ,
,
∴点H是△ABD的外心,点H是△BCD的外心,点H是△ADC的外心,所以②③④正确.
故选:C.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】下表给出了代数式ax2+bx+c与x的一些对应值:
x | … | 0 | 1 | 2 | 3 | 4 | … |
ax2+bx+c | … | 3 |
| ﹣1 |
| 3 | … |
(1)请在表内的空格中填入适当的数;
(2)设y=ax2+bx+c,则当x取何值时,y<0;
(3)当0<x<3,求x的取值范围.
【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.4 | 4.3 | ||
卡路里消耗(千卡) | 157 | 79 | 91 | 127 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
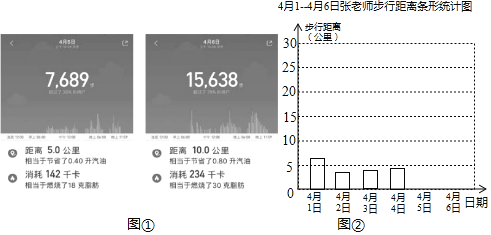
(1)请你将手环记录的4月5日和4月6日的数据(如图①)填入表格
(2)请你将条形统计图(如图②)补充完整
(3)张老师这6天平均每天步行约______公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为______公里(精确到0.1公里)
【题目】某品牌电脑销售公司有营销员14人,销售部为制定营销人员月销售电脑定额,统计了这14人某月的销售量如下(单位:台):
销售量 | 200 | 170 | 130 | 80 | 50 | 40 |
人数 | 1 | 1 | 2 | 5 | 3 | 2 |
(1)该公司营销员销售该品牌电脑的月销售平均数是 台,中位数是 台,众数是 台.
(2)销售部经理把每位营销员月销售量定为90台,你认为是否合理?说明理由.