题目内容
【题目】
特例研究：如图
，等边
的边长为8，求等边的高．
经验提升：
如图
，在中，
，点P为射线BC上的任一点，过点P作
，
，垂足分别为D、E，过点C作
，垂足为
补全图形，判断线段PD，PE，CF的数量关系，并说明理由．
综合应用：
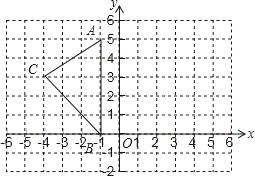
如图
，在平面直角坐标系中有两条直线
：
，
：
，若线段BC上有一点M到的距离是1，请运用中的结论求出点M的坐标．
【答案】(1)
；(2)见解析;(3)
坐标为
．
【解析】
利用等边三角形的性质和勾股定理即可得出结论；
利用面积法可以证明结论；
连接AP，同理利用
与
面积之差等于
的面积可以证得结论；
根据题意得到
，
，
，
，根据图的结论，求得M到AC的距离，即M点的纵坐标，再代入
的解析式可求出M的坐标．
解：如图
，过点A作
于G，
是等边三角形，
，
在
中，
，
，
则等边的高为；当点P在边BC上时，
，
理由如下：如图，连接AP，
，
，
，
，
，
，
，
，
，
；当点P在BC的延长线上时，
，
理由如下：如图
，连接AP，
，，，，，，
，
，，
；如图
，由题意可求得
，
，
，
，，
，，
过M分别作
轴，
，垂足分别为P、Q，
上的一点M到
的距离是1，
，
由图的结论得：
，
，
点的纵坐标为2，
在直线
，
当
时，
，坐标为．
走进文言文系列答案
【题目】2019年元旦期间，某超市打出促销广告，如下表所示：
一次性所购物品的原价 | 优惠办法 |
不超过200元 | 没有优惠 |
超过200元，但不超过600元 | 全部按九折优惠 |
超过600元 | 其中600元仍按九折优惠，超过600元部分按8折优惠 |
（1）小张一次性购买物品的原价为400元，则实际付款为 元；
（2）小王购物时一次性付款580元，则所购物品的原价是多少元？
（3）小赵和小李分别前往该超市购物，两人各自所购物品的原价之和为1200元，且小李所购物品的原价高于小赵，两人实际付款共1074元，则小赵和小李各自所购物品的原价分别是多少元？
【题目】某校八年级学生开展跳绳比赛活动，每班派5名学生参加，按团体总分多少排列名次，统计发现成绩最好的甲班和乙班总分相等，下表是甲班和乙班学生的比赛数据
单位：个
选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 总计 |
甲班 | 100 | 98 | 105 | 94 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
此时有学生建议，可以通过考察数据中的其他信息作为参考，请解答下列问题：
求两班比赛数据中的中位数，以及方差；
请根据以上数据，说明应该定哪一个班为冠军？为什么？
