题目内容
(Figure 1) In the parallelogram ABCD,AD=2AB,a
point M is mid- point of segment AD,CE⊥AB,if∠CEM=40°,then the value of∠DME it( ).
(A)150° (B)140° (C)135° (D)130°
如图,连接CM,作MN⊥EC于N.
∵ AB⊥CE ∴MN∥AB,且MN∥CD,从N为梯形AECD的中位数.
由MN⊥CE,MN是EC边中线,∴△EMC为等腰△,
∴∠ECM=∠MEC=40° ∠EMC=180°-2×40°=100°
∵ ∠ECD=∠AEC=90°,∴∠MCD=90°-40°=50°,
又∵ DC=
AD=DM,∴∠MCD=∠DMC=50°,∴
∠EMD=∠EMC+∠CMD=100°+50°=150°.选(A)
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
If the figure 6 is composed of 24 equilateral triangles，then how many non-congruent distinct right triangles with vertices on the intersecting points are possible in this figure（ ）
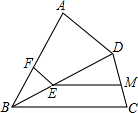In fig 1，ABCD is a quadrilsteral，E is a point the diagonal BD，EF∥AD，EM∥BC，then the value of | EF |
| DA |
| EM |
| BC |
（英汉词典：fig figure的缩写，图；quadrilateral四边形；diagonal对角线；value数值；variable变量；to depend on取决于；position位置）
四边形ABCD中，E是对角线BD上一点，EF∥AD，EM∥BC，则
| EF |
| DA |
| EM |
| BC |
| A、greater than 1（大于1） |
| B、equal to 1（等于1） |
| C、less than 1（小于1） |
| D、variable depending on the position of E（不能确定，与E的位置有关） |
As in figure 2．In the circular ring of which center is point O．if AO⊥BO，and the area of the shadowy part is 25cm2，then the area of the circuiar ring equals to（ ） （π≈3.14）