题目内容
20．甲乙两人玩“石头、剪子、布”游戏，他们在不透明的袋子中放入形状、大小均相同的10张卡片，其中写有“石头”“剪子”“布”的卡片数分别为2、3、5，两人各随机摸出一张卡片（先摸者不放回）来比胜负，并约定：“石头”胜“剪子”，“剪子”胜“布”，“布”胜“石头”，同种卡片不分胜负．（1）若甲先摸，他摸出“石头”的概率是多少？
（2）若甲先摸出了“石头”，则乙获胜的概率是多少？
分析 （1）直接根据概率公式求解；
（2）先画树状图展示所有9种可能的结果数，找出“布”胜“石头”的结果数，然后根据概率公式求解．
解答 解：（1）若甲先摸，他摸出“石头”的概率是$\frac{2}{10}$=$\frac{1}{5}$；
（2）画树状图为：
共有9种可能的结果数，其中乙获胜的结果数为5，
所以若甲先摸出了“石头”，则乙获胜的概率是$\frac{5}{9}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
相关题目
10．某天放学后，小敏徒步回家，如图所示，反映了她的速度与时间的变化关系．
（1）请你根据图象填写下表：
（2）根据图象或表格你能叙述一下小敏行走的情况吗？
（1）请你根据图象填写下表：
| 时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
| 速度/（千米/时） |
如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，-3）．反比例函数y1=$\frac{k}{x}$图象经过点C，一次函数y2=ax+b的图象经过点A、C
8．
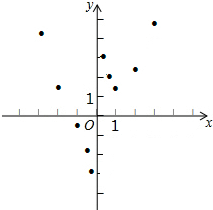有这样一个问题：探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质．
小东根据学习函数的经验，对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
求m的值；
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）该函数没有最大值．
有这样一个问题：探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质．小东根据学习函数的经验，对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究．
下面是小东的探究过程，请补充完整：
（1）函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0；
（2）下表是y与x的几组对应值．
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
（3）如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
（4）进一步探究发现，该函数图象在第一象限内的最低点的坐标是（1，$\frac{3}{2}$），结合函数的图象，写出该函数的其它性质（一条即可）该函数没有最大值．
在△ABC中，∠BAC=110°，∠ACB的平分线交AB于点D，且∠CAE=40°，连接DE，则∠EDC的度数是20°．
5．正n边形每个内角的大小都为108°，则n=（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
在平行四边形ABCD中，E为BC边上的一点．连结AE．