题目内容
设g(x)=3x2-2x+1,f(x)=x3-3x2-x-1,求用g(x)去除f(x)所得的商q(x)及余式r(x).
由于f(x)为3次多项式,首项系数为1,而g(x)为2次,首项系数为3,故商q(x)必为1次,首项的系数必为
,而余式次数小于2,于是可设商式q(x)=
+a,余式r(x)=bx+c.
根据f(x)=q(x)g(x)+r(x),得
x3-3x2-x-1=(3x2-2x+1)(
x+a)+(bx+c)=x3+(3a-
)x2+(b-2a+
)+(a+c)
比较两端系数,得
1,
解得a=-
,b=-
,c=-
,故商式q(x)=
x-
,余式r(x)=-
x-
.
| 1 |
| 3 |
| 1 |
| 3 |
根据f(x)=q(x)g(x)+r(x),得
x3-3x2-x-1=(3x2-2x+1)(
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
比较两端系数,得
|
解得a=-
| 7 |
| 9 |
| 26 |
| 9 |
| 2 |
| 9 |
| 1 |
| 3 |
| 7 |
| 9 |
| 26 |
| 9 |
| 2 |
| 9 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
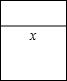 用18米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )
用18米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )