题目内容
 某小区为了改善居住环境,准备修建一个矩形花园ABCD,为了节约材料并种植不同类花,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块,已知所用栅栏的总长为60米,墙长为30米(如图),设花园垂直于墙的一边的长为x米.
某小区为了改善居住环境,准备修建一个矩形花园ABCD,为了节约材料并种植不同类花,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块,已知所用栅栏的总长为60米,墙长为30米(如图),设花园垂直于墙的一边的长为x米.
(1)若平行于墙的一边长为y米,直接写出y与x的函数关系式及自变量x的取值范围;
(2)当x为何值时,这个矩形花园的面积最大?最大值是多少?(栅栏占地面积忽略不计);
(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出x的取值范围.
 解:(1)∵60=AB+CD+EFBC,AB=EF=CD=x,BC=y,
解:(1)∵60=AB+CD+EFBC,AB=EF=CD=x,BC=y,∴3x+y=60,
∴y=-3x+60(10≤x<20);
(2)∵S=xy=x(-3x+60),
∴S=-3x2+60x,
∵a=-3<0,
∴当x=-
 =10时,S有最大值
=10时,S有最大值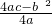 =300平方米;
=300平方米;
(3)∵这个花园的面积不小288平方米,
∴-3x2+60x≥288,
∴-3x2+60x-288≥0.
设y=-3x2+60x-288≥0.
此函数的图象如图所示:
∴当这个花园的面积不小288平方米时,出x的取值范围是:10≤x≤12.
分析:(1)由题意可知栅栏的总长60米可以看做有BC,AB,CD和EF四段组成,把已知数据代入即可求出y和x的函数关系;
(2)利用矩形的面积公式:长×宽和(1)的结论即可得到S和x的关系式,再利用二次函数的性质即可求出当x为何值时,这个矩形花园的面积最大和其最大值;
(3)由(2)可知函数的关系式,由此关系式画出函数的图象,结合图象可直接写出x的取值范围.
点评:本题考查的是二次函数的实际应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

练习册系列答案
相关题目
某地区为了改善生态环境,增加农民收入,自2004年起就鼓励农民在荒山上广泛种植某种果树,并且出台了一项激励措施:即在开荒种树的过程中,每一年新增果树达到100棵的农户,当年都可得到生活补贴1200元,且每超出一棵,政府还给予每棵a元的奖励.另外,种植的果树,从下一年起,每年每棵平均将有b元的果实收入.下表是某农户在头两年通过开荒种树每年获得的总收入情况:
(注:年总收入=生活补贴费+政府奖励费+果实收入)
(1)试根据以上提供的资料确定a、b的值;
(2)从2006年起,该农户每年新增果树的棵数将以相同的百分率增长,预计2007年新增果树216棵,那么2007年该农户通过种植果树获得的年总收入将达到多少元?
| 年份 | 新果树的棵树 | 年总收入 |
| 2004年 | 130棵 | 1500元 |
| 2005年 | 150棵 | 4300元 |
(1)试根据以上提供的资料确定a、b的值;
(2)从2006年起,该农户每年新增果树的棵数将以相同的百分率增长,预计2007年新增果树216棵,那么2007年该农户通过种植果树获得的年总收入将达到多少元?
某地区为了改善生态环境,增加农民收入,自2004年起就鼓励农民在荒山上广泛种植某种果树,并且出台了一项激励措施:即在开荒种树的过程中,每一年新增果树达到100棵的农户,当年都可得到生活补贴1200元,且每超出一棵,政府还给予每棵a元的奖励.另外,种植的果树,从下一年起,每年每棵平均将有b元的果实收入.下表是某农户在头两年通过开荒种树每年获得的总收入情况:
| 年份 | 新果树的棵树 | 年总收入 |
| 2004年 | 130棵 | 1500元 |
| 2005年 | 150棵 | 4300元 |
(1)试根据以上提供的资料确定a、b的值;
(2)从2006年起,该农户每年新增果树的棵数将以相同的百分率增长,预计2007年新增果树216棵,那么2007年该农户通过种植果树获得的年总收入将达到多少元?
