题目内容
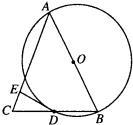24、如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC于E．（1）求证：AB=AC；（2）求证：DE为⊙O的切线．
分析：（1）连接AD，根据中垂线定理不难求得AB=AC；
（2）要证DE为⊙O的切线，只要证明∠ODE=90°即可．
（2）要证DE为⊙O的切线，只要证明∠ODE=90°即可．
解答：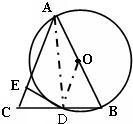
证明：（1）连接AD；
∵AB是⊙O的直径，
∴∠ADB=90°．
又∵DC=BD，
∴AD是BC的中垂线．
∴AB=AC．
（2）连接OD；
∵AB=AC，AD⊥BC，
∴∠EAD=∠BAD．
又∵OA=OD，
∴∠BAD=∠ODA．
∴∠EAD=∠ODA．
∴OD∥AC．
又∵DE⊥AC，
∴∠ODE=∠AED=90°．
∴DE为⊙O的切线．
证明：（1）连接AD；∵AB是⊙O的直径，
∴∠ADB=90°．
又∵DC=BD，
∴AD是BC的中垂线．
∴AB=AC．
（2）连接OD；
∵AB=AC，AD⊥BC，
∴∠EAD=∠BAD．
又∵OA=OD，
∴∠BAD=∠ODA．
∴∠EAD=∠ODA．
∴OD∥AC．
又∵DE⊥AC，
∴∠ODE=∠AED=90°．
∴DE为⊙O的切线．
点评：此题主要考查了切线的判定，等腰三角形的性质及圆周角的性质等知识点的综合运用．
练习册系列答案
相关题目
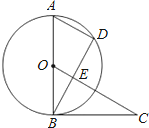如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A．
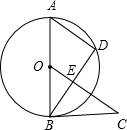如图所示，AB是⊙O的直径，AD是弦，∠DBC=∠A，OC⊥BD于点E．
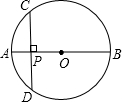如图所示，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，则⊙O的半径为
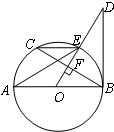如图所示，AB是⊙O直径，OD⊥弦BC于点F，且交⊙O于点E，且∠AEC=∠ODB．
如图所示，AB是⊙O直径，∠D=35°，则∠BOC等于（ ）