题目内容
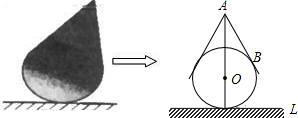
如图，将一个圆锥沿母线AB展开后得到一个扇形，（1）若圆锥的高AO为2
| 2 |
（2）若扇形的弧（
 |
| AB |
分析：（1）首先根据圆锥的高和底面半径求得圆锥的母线长，然后利用扇形的面积求得扇形的面积即可；
（2）表示出圆锥的母线长，然后列出等式求解即可．
（2）表示出圆锥的母线长，然后列出等式求解即可．
解答：解：（1）∵圆锥的高AO为2
，底面半径为1，
∴圆锥的母线长为3，
∴圆锥的侧面积为πrl=π×1×3=3π；
（2）设圆锥的母线长为l，根据题意得：AB=AC=l，
所以2πr=2l
所以
=π；
| 2 |
∴圆锥的母线长为3，
∴圆锥的侧面积为πrl=π×1×3=3π；
（2）设圆锥的母线长为l，根据题意得：AB=AC=l，
所以2πr=2l
所以
| l |
| r |
点评：本题考查了圆锥的计算，解题的关键是弄清圆锥和扇形的有关量的对应．
练习册系列答案
名校课堂系列答案
相关题目
纸帽的表面全涂上颜色，则需要涂色部分的面积约为
13、如图，将一个底面直径为2cm，高为2cm的圆柱形纸筒沿一条母线剪开，所得到的侧面展开图的面积为（ ）
如图，将一个圆锥沿母线AB展开后得到一个扇形，
如图，将一个圆锥沿母线AB展开后得到一个扇形，
，底面半径为1，求扇形的面积；
）长恰好等于圆锥母线AB和AC的长度之和，求圆锥的母线AB与地面圆半径OB之比．