Question

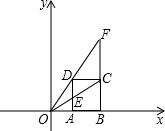（2013•南平模拟）在平面直角坐标系xOy中，矩形ABCD如图放置，边AB在x轴上，点A坐标为（1，0），点C坐标为（3，m）（m＞0）．连接OC交AD与E，射线OD交BC延长线于F．
（1）求点E、F的坐标﹔
（2）当x的值改变时：
①证明﹕经过O、E、F三点的抛物线的最低点一定为原点﹔
②设经过O、E、F三点的抛物线与直线CD的交点为P，求PD的长﹔
③探究﹕△ECF能否成为等腰三角形？若能，请求出△ECF 的面积．

Answer 1

分析：（1）根据相似三角形的判定和性质即可求出点E、F的坐标﹔
（2）①二次函数的图象经过坐标原点O，可设二次函数为y=ax²+bx，根据待定系数法求出二次函数的解析式，即可证明经过O、E、F三点的抛物线的最低点一定为原点﹔
②根据纵坐标相等可得方程，求得x的值，从而得到PD的长﹔
③根据等腰三角形的性质可得关于m的方程，求得m的值，再根据三角形的面积公式即可求解．

解答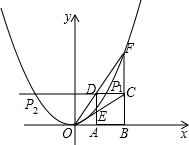：（1）解：∵点A坐标为（1，0），点C坐标为（3，m），
∴OA=1，OB=3，BC=AD=m，
∵AE∥BC，
∴△OAE∽△OBC，
∴

OA

OB

=

AE

BC

，即AE=

OA•BC

OB

=

m

3

，
∴点E坐标为（1，

m

3

），
同理，得△OAD∽△OBF，
∴

OA

OB

=

AD

BF

，即BF=

OB•AD

OA

=3m，
∴点F坐标为（1，3m）；

（2）证明：∵二次函数的图象经过坐标原点O，
∴设二次函数为y=ax²+bx，
又∵二次函数的图象经过E、F，
∴

a+b= m 3 9a+3b=3m

，
解得

a= m 3 b=0

．
∴二次函数的解析式为y=

m

3

x²，
∴抛物线的最低点一定为原点﹔
②解：∵m=

m

3

x²，
解得x=±

3

，
∴PD的长为

3

-1，

3

+1；
③答：能．
∵∠ECF为钝角，
∴仅当EC=FC时，△ECF为等腰三角形，
由EC²=FC²，得CD²+ED²=FC²，
即2²+（m-

m

3

）²=（3m-m）²，
解得m=±

3

4

2

，
∵m＞0，
∴m=

3

4

2

，
∴△ECF的面积=

1

2

FC•CD=

1

2

×2m×2=

3

2

2

．

点评：考查了二次函数综合题，涉及的知识点有：平行线的性质，相似三角形的判定和性质，待定系数法求二次函数的解析式，等腰三角形的性质，三角形的面积，方程思想的运用，综合性较强，有一定的难度．