题目内容
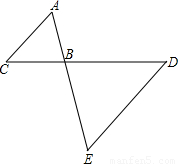
 如图,已知AE与CD交于点B,AC∥DE.
如图,已知AE与CD交于点B,AC∥DE.求证:(1)△ABC∽△EBD;(2)若AC=3,BC=4,BD=8,求DE的长.
分析:(1)由平行于三角形一边的直线截另两边所得三角形与原三角形相似,即可证得:△ABC∽△EBD;
(2)由相似三角形的对应边成比例,即可求得DE的长.
(2)由相似三角形的对应边成比例,即可求得DE的长.
解答:(1)证明:∵AC∥DE,
∴△ABC∽△EBD(平行于三角形一边的直线截另两边所得三角形与原三角形相似);
(2)解:∵△ABC∽△EBD,
∴
=
(相似三角形的对应边成比例),
∵AC=3,BC=4,BD=8,
∴DE=6.
∴△ABC∽△EBD(平行于三角形一边的直线截另两边所得三角形与原三角形相似);
(2)解:∵△ABC∽△EBD,
∴
| AC |
| ED |
| BC |
| BD |
∵AC=3,BC=4,BD=8,
∴DE=6.
点评:此题考查了相似三角形的判定(平行于三角形一边的直线截另两边所得三角形与原三角形相似)与性质(相似三角形的对应边成比例).此题很简单,解题时要注意细心.

练习册系列答案
相关题目
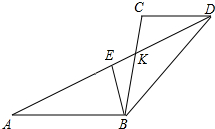 如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.
如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点. 如图,已知AE与CD交于点B,AC∥DE.
如图,已知AE与CD交于点B,AC∥DE.