题目内容
如图1,已知⊙O的半径是2,C为直径BA延长线上一点,OC=4,过C作直线CF使∠OCF=30°.
(1)求证:⊙O与直线CF相切;
(2)如图2,设(1)中的切点为E,Q为圆周上一点,EQ交AB于D,cos∠AEQ=
,求
的值;
(3)如图3,设P为线段AC上的一个动点(不与A、C重合),求证:不论P在何处,总存在弦EQ(EQ与AB交于D)使得ED•QD=AP•PC成立.
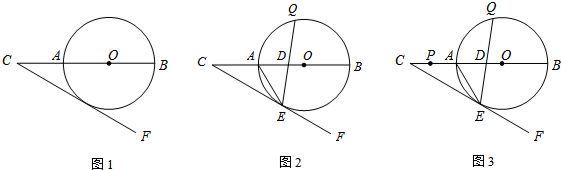
(1)求证:⊙O与直线CF相切;
(2)如图2,设(1)中的切点为E,Q为圆周上一点,EQ交AB于D,cos∠AEQ=
| 3 |
| 4 |
| BD |
| DE |
(3)如图3,设P为线段AC上的一个动点(不与A、C重合),求证:不论P在何处,总存在弦EQ(EQ与AB交于D)使得ED•QD=AP•PC成立.

考点:圆的综合题
专题:
分析:(1)过O作OE⊥CF于E,根据∠OCF=30°,可知OE=
=2,再根据⊙O的半径是2即可得出结论;
(2)连结QA、QB,根据OA=AC=2,△COE是直角三角形可得出AE的长,再由cos∠AEQ=
得出cos∠ABQ=
,AB=4,BQ=3,由相似三角形的判定定理得出△AED∽△BQD,根据相似三角形的对应边成比例得出
=
=
;
(3)设AP=a(0<a<2),AD=x,则BD=4-x,令x(4-x)=a(2-a),即x2-4x+2a-a2=0,根据△=4(4-2a+a2)>0可知方程总有解,即不论P在何处,AD×BD=AP×PC总能成立,再根据△AED∽△BQD可得出ED×QD=AD×BD,故可得出结论.
| AB |
| 2 |
(2)连结QA、QB,根据OA=AC=2,△COE是直角三角形可得出AE的长,再由cos∠AEQ=
| 3 |
| 4 |
| 3 |
| 4 |
| BD |
| DE |
| QB |
| AE |
| 3 |
| 2 |
(3)设AP=a(0<a<2),AD=x,则BD=4-x,令x(4-x)=a(2-a),即x2-4x+2a-a2=0,根据△=4(4-2a+a2)>0可知方程总有解,即不论P在何处,AD×BD=AP×PC总能成立,再根据△AED∽△BQD可得出ED×QD=AD×BD,故可得出结论.
解答:解: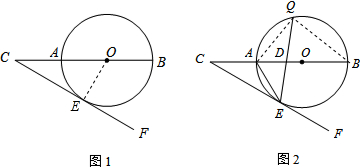 (1)过O作OE⊥CF于E,
(1)过O作OE⊥CF于E,
∵∠OCF=30°,
∴OE=
=2
又∵⊙O的半径是2,
∴⊙O与CF相切;
(2)连结QA、QB,
∵OA=AC=2,△COE是直角三角形,
∴AE=
=2,
∵cos∠AEQ=
,
∴cos∠ABQ=
,AB=4,
∴BQ=3,
∵∠AED=∠DBQ,∠ADE=∠BDQ,
∴△AED∽△BQD,
∴
=
=
;
(3)设AP=a(0<a<2),AD=x,则BD=4-x,令x(4-x)=a(2-a),即x2-4x+2a-a2=0,
∵△=4(4-2a+a2)>0,
∴方程总有解,即不论P在何处,AD×BD=AP×PC总能成立,
又∵△AED∽△BQD,
∴ED×QD=AD×BD,
∴不论P在何处,总存在弦EQ使得ED×QD=AP×PC成立.
 (1)过O作OE⊥CF于E,
(1)过O作OE⊥CF于E,∵∠OCF=30°,
∴OE=
| AB |
| 2 |
又∵⊙O的半径是2,
∴⊙O与CF相切;
(2)连结QA、QB,
∵OA=AC=2,△COE是直角三角形,
∴AE=
| OC |
| 2 |
∵cos∠AEQ=
| 3 |
| 4 |
∴cos∠ABQ=
| 3 |
| 4 |
∴BQ=3,
∵∠AED=∠DBQ,∠ADE=∠BDQ,
∴△AED∽△BQD,
∴
| BD |
| DE |
| QB |
| AE |
| 3 |
| 2 |
(3)设AP=a(0<a<2),AD=x,则BD=4-x,令x(4-x)=a(2-a),即x2-4x+2a-a2=0,
∵△=4(4-2a+a2)>0,
∴方程总有解,即不论P在何处,AD×BD=AP×PC总能成立,
又∵△AED∽△BQD,
∴ED×QD=AD×BD,
∴不论P在何处,总存在弦EQ使得ED×QD=AP×PC成立.
点评:本题考查的是圆的综合题,涉及到相似三角形的判定与性质、切线的判定、锐角三角函数的定义及圆周角定理等知识,难度适中.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,已知a∥b,c∥d,∠1=70°,求∠2、∠3的度数.
如图,已知a∥b,c∥d,∠1=70°,求∠2、∠3的度数.