题目内容
(2013年四川眉山3分)如图,在函数 (x<0)和
(x<0)和 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC= ,S△BOC=
,S△BOC=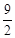 ,则线段AB的长度= .
,则线段AB的长度= .

 (x<0)和
(x<0)和 (x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC=
(x>0)的图象上,分别有A、B两点,若AB∥x轴,交y轴于点C,且OA⊥OB,S△AOC= ,S△BOC=
,S△BOC=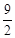 ,则线段AB的长度= .
,则线段AB的长度= .
 。
。∵S△AOC= ,S△BOC=
,S△BOC=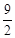 ,∴
,∴ |k1|=
|k1|= ,
, |k2|=
|k2|=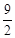 。∴k1=﹣1,k2=9。,
。∴k1=﹣1,k2=9。,
∴两反比例解析式为 ,
, 。
。
设B点坐标为( ,t)(t>0),
,t)(t>0),
∵AB∥x轴,∴A点的纵坐标为t。
把y=t代入 得
得 。∴A点坐标为(
。∴A点坐标为( ,t)。
,t)。
∵OA⊥OB,∴∠AOC=∠OBC。∴Rt△AOC∽Rt△OBC。
∴OC:BC=AC:BC,即t: =
= :t,解得∴t=
:t,解得∴t= 。
。
∴A点坐标为( ,
, ),B点坐标为(3
),B点坐标为(3 ,
, )。
)。
∴线段AB的长度=3 ﹣(
﹣( )=
)= 。
。
 ,S△BOC=
,S△BOC=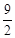 ,∴
,∴ |k1|=
|k1|= ,
, |k2|=
|k2|=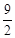 。∴k1=﹣1,k2=9。,
。∴k1=﹣1,k2=9。,∴两反比例解析式为
 ,
, 。
。设B点坐标为(
 ,t)(t>0),
,t)(t>0),∵AB∥x轴,∴A点的纵坐标为t。
把y=t代入
 得
得 。∴A点坐标为(
。∴A点坐标为( ,t)。
,t)。∵OA⊥OB,∴∠AOC=∠OBC。∴Rt△AOC∽Rt△OBC。
∴OC:BC=AC:BC,即t:
 =
= :t,解得∴t=
:t,解得∴t= 。
。∴A点坐标为(
 ,
, ),B点坐标为(3
),B点坐标为(3 ,
, )。
)。∴线段AB的长度=3
 ﹣(
﹣( )=
)= 。
。
练习册系列答案
相关题目
 的两条直角边之比为
的两条直角边之比为 ,△
,△ ∽△
∽△ ,若△
,若△ ,则△
,则△ .
.