Question

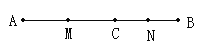
【题目】已知，、在数轴上对应的数分别用、表示，且．

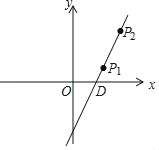
（1）数轴上点表示的数是________，点表示的数是___________；

（2）若一动点从点出发，以个单位长度秒速度由向运动；动点从原点出发，以个单位长度秒速度向运动，点、同时出发，点运动到点时两点同时停止．设点运动时间为秒．

①若从到运动，则点表示的数为_______，点表示的数为___________（用含的式子表示）

②当为何值时，点与点之间的距离为个单位长度．

Answer 1

【答案】（1）-5，15；（2）①-5+3t，t；②当=1.5或3.5秒．

【解析】

（1）根据偶数次幂和绝对值的非负性，即可求解；

（2）①根据点P与点Q的移动速度和起始位置，即可得到答案；②分两种情况讨论：若点P在点的左边时，若点P在点的右边时，分别列出关于t的方程，即可求解．

（1）∵，

又∵，

∴，

解得：a=-5，b=15；

∴数轴上点表示的数是-5，点表示的数是15．

故答案是：-5，15；

（2）①∵点P以个单位长度/秒速度由向运动,

∴点表示的数为：-5+3t，

∵动点从原点出发，以个单位长度秒速度向运动，

∴点表示的数为：t．

故答案是：-5+3t，t；

②若点P在点的左边时，t-(-5+3t)=2，解得：t=1.5；

若点P在点的右边时，(-5+3t)-t=2，解得：t=3.5．

答：当=1.5或3.5秒时，点与点之间的距离为个单位长度．