题目内容
19.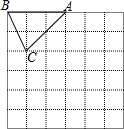 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算点C在变换到点C2的过程中经过的路线长;
(3)计算线段B1C1在变换到线段B2C2的过程中扫过的图形的面积.
分析 (1)直接利用平移的性质以及结合旋转的性质得出对应点位置进而得出答案;
(2)利用弧长公式得出以及平移的性质得出点C在变换到点C2的过程中经过的路线长;
(3)直接利用线段B1C1在变换到线段B2C2的过程中扫过的图形的面积为S扇形A1B1B2-S扇形C1A1C2即可得出答案.
解答 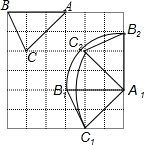 解:(1)如图所示:△A1B1C1和△A1B2C2,即为所求;
解:(1)如图所示:△A1B1C1和△A1B2C2,即为所求;
(2)点C在变换到点C2的过程中经过的路线长为:4+3+$\frac{90π×2\sqrt{2}}{180}$=7+$\sqrt{2}$π;
(3)线段B1C1在变换到线段B2C2的过程中扫过的图形的面积为:$\frac{90π×{3}^{2}}{360}$-$\frac{90π×(2\sqrt{2})^{2}}{360}$=$\frac{π}{4}$.
点评 此题主要考查了旋转变换以及平移变换和扇形面积公式以及弧长公式,正确得出旋转后对应点位置是解题关键.

练习册系列答案
相关题目
13.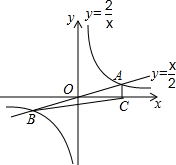 如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
 如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )
如图,正比例函数y=$\frac{x}{2}$与反比例函数y=$\frac{2}{x}$的图象交于A,B两点,AC⊥x轴于点C,连接BC,则△BOC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 1 |
7. 小江玩投掷飞镖的游戏,他设计了一个如图所示的靶子,E,F分别是矩形ABCD的边AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N.连接AM,CN,MN,则投掷一次,飞镖落在阴影部分的概率是( )
小江玩投掷飞镖的游戏,他设计了一个如图所示的靶子,E,F分别是矩形ABCD的边AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N.连接AM,CN,MN,则投掷一次,飞镖落在阴影部分的概率是( )
 小江玩投掷飞镖的游戏,他设计了一个如图所示的靶子,E,F分别是矩形ABCD的边AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N.连接AM,CN,MN,则投掷一次,飞镖落在阴影部分的概率是( )
小江玩投掷飞镖的游戏,他设计了一个如图所示的靶子,E,F分别是矩形ABCD的边AB,CD的中点,连接DE和BF,分别取DE,BF的中点M,N.连接AM,CN,MN,则投掷一次,飞镖落在阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
14.一个骰子,六个面上的数字分别为1、2、3、4、5、6,连续投掷两次,两次向上的面出现数字之和为偶数的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
9.某市2016年参加中考的考生人数约为85000人,将85000用科学记数法表示为( )
| A. | 8.5×104 | B. | 8.5×105 | C. | 0.85×104 | D. | 0.85×105 |