题目内容
 如图,图①中圆与正方形各边都相切,设这个圆的周长为C1;图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长为C2;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长为C3;…,依次规律,当正方形边长为2时,则C1+C2+C3+…C99+C100=
如图,图①中圆与正方形各边都相切,设这个圆的周长为C1;图②中的四个圆的半径相等,并依次外切,且与正方形的边相切,设这四个圆的周长为C2;图③中的九个圆的半径相等,并依次外切,且与正方形的边相切,设这九个圆的周长为C3;…,依次规律,当正方形边长为2时,则C1+C2+C3+…C99+C100=10100π
10100π
.分析:根据圆的周长公式求出C1=2π×1,C2=2π×2;,C3=2π×3;推出C100=2π×100,代入C1+C2+C3+…+C99+C100,得出2π×1+2π×2+2π×3+2π×4+…+2π×99+2π×100,求出即可.
解答:解:C1=2π×
×2=2π=2π×1;
C2=2π×
×
×2×4=4π=2π×2;
C3=2π×
×
×2×9=6π=2π×3;
C4=2π×
×
×2×16=8π=2π×4;
…
C100=2π×100=200π,
∴C1+C2+C3+…+C99+C100
=2π×1+2π×2+2π×3+2π×4+…+2π×99+2π×100
=2π(1+2+3+4+…+99+100)
=10100π.
故答案为:10100π.
| 1 |
| 2 |
C2=2π×
| 1 |
| 2 |
| 1 |
| 2 |
C3=2π×
| 1 |
| 3 |
| 1 |
| 2 |
C4=2π×
| 1 |
| 4 |
| 1 |
| 2 |
…
C100=2π×100=200π,
∴C1+C2+C3+…+C99+C100
=2π×1+2π×2+2π×3+2π×4+…+2π×99+2π×100
=2π(1+2+3+4+…+99+100)
=10100π.
故答案为:10100π.
点评:本题考查了相切两圆的性质和图形的变化类的应用,关键是根据求出的结果得出规律(Cn=2π×n),题型较好,有一点难度.

练习册系列答案
相关题目
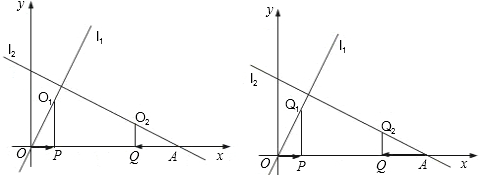 ,求出t值;若不能,说明理由.(同学可在图2中画草图)
,求出t值;若不能,说明理由.(同学可在图2中画草图)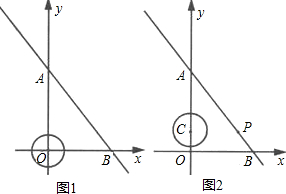 以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;
以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;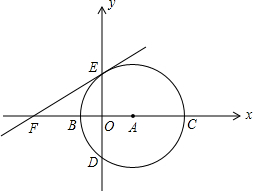 于B、C两点,与y轴相交于D、E两点.
于B、C两点,与y轴相交于D、E两点.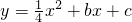 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上? ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由; ?若能,请直接写出Q点坐标;若不能,请说明理由.
?若能,请直接写出Q点坐标;若不能,请说明理由. 经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上?
经过C、D两点,求此抛物线的解析式,并判断点B是否在这条抛物线上? ,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由;
,0),求此直线的解析式,这条直线是⊙A的切线吗?请说明理由; ?若能,请直接写出Q点坐标;若不能,请说明理由.
?若能,请直接写出Q点坐标;若不能,请说明理由.
 ,并且与x轴、y轴分别交于点A、B.
,并且与x轴、y轴分别交于点A、B.