题目内容
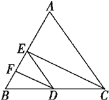
如图，在△ABC中，CE⊥AB于点E，DF⊥AB于点F，CE平分∠ACB，DF平分∠BDE，
求证：AC∥ED.
证明：∵CE⊥AB于E，DF⊥AB于F（已知）
∴DF∥ （垂直于同一条直线的两直线平行）
∴∠BDF=∠ （ ）
∠FDE=∠ （两直线平行，内错角相等）
∵CE平分∠ACB，DF平分∠BDE（已知）
∴∠ACE=∠ECB，∠EDF=∠BDF（角平分线的定义）
∴∠ACE=∠ （等量代换）
∴AC∥ED（ ）.
练习册系列答案
应用题作业本系列答案
相关题目
的算术平方根是_____．
＋
=0,（c－4）2≤0.
），请用含m的式子表示四边形ABOP的面积． 
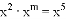，则m=___________.