题目内容
【题目】如图，平行四边形
的对角线
交于点
，点
在边
的延长线上，且
．
（1）求证：四边形是矩形；
（2）延长
交于点
，若
，求证：
．
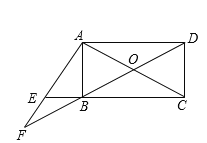
【答案】（1）证明见解析；（2）证明见解析．
【解析】
（1）根据AE2=EBEC证明△AEB∽△CEA，即可得到∠EBA=∠EAC=90°，从而说明平行四边形ABCD是矩形；
（2）根据（1）中△AEB∽△CEA可得
，再证明△EBF∽△BAF可得
，结合条件AF=AC，即可证AE=BF．
证明：（1）∵
∴
又 ∵
∴
∽
∴
∵
∴
又 ∵
∴
∵四边形ABCD是平行四边形
∴四边形ABCD是矩形
（2）∵ ∽
∴ 
即 ， 
∵四边形ABCD是矩形
∴
又∵
，
∴
∴
又 ∵
，
∴
又 ∵
∴
∽
∴
∴
∵
∴
，即
练习册系列答案
名校课堂系列答案
相关题目
【题目】某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
（1）这天部分出行学生使用共享单车次数的中位数是 ，众数是 ．
（2）这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）
（3）若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少名．
