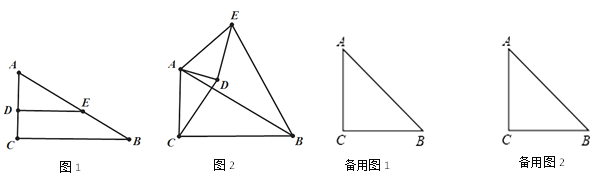
题目内容
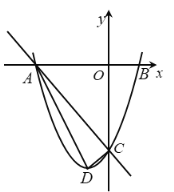
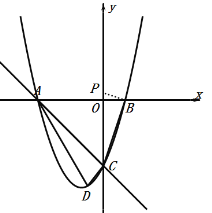
【题目】如图,顶点为![]() 的抛物线
的抛物线![]() 与交
与交![]() 轴分别于点
轴分别于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),与交
的左侧),与交![]() 轴交于点
轴交于点![]() .已知直线
.已知直线![]() 的解析式为
的解析式为![]() .
.
(1)求抛物线的解析式:
(2)若以点![]() 为圆心的圆与
为圆心的圆与![]() 相切,求
相切,求![]() 的半径;
的半径;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似?如果存在,请求出点
相似?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)在
;(3)在![]() 轴上存在一点
轴上存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似,点
相似,点![]() 的坐标是
的坐标是![]() 或
或![]()
【解析】
(1)利用直线![]() 的解析式
的解析式![]() 分别求得A、C的坐标,利用待定系数法即可求得抛物线的解析式;
分别求得A、C的坐标,利用待定系数法即可求得抛物线的解析式;
(2)利用两点之间的距离公式,分别求得AD、AC、CD的长,根据勾股定理的逆定理先判断出△ADC是直角三角形,再利用面积法即可求解;
(3)分三种情况讨论,利用相似三角形对应边成比例即可求解.
(1)把![]() 代入
代入![]() ,得
,得![]() .
.
∴![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() ,
,
把![]() ,
,![]() ,
,![]() 代入
代入![]() ,得
,得
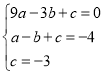 ,解得
,解得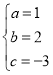 ,
,
∴抛物线的解析式为:![]() ;
;
(2)∵![]() ,
,![]() ,
,![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
同理:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是直角三角形,
是直角三角形,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
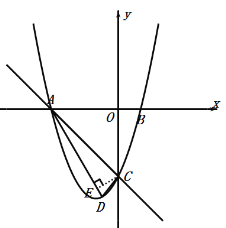
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的半径为
的半径为![]() ;
;
(3)答:在![]() 轴上存在一点
轴上存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似.
相似.
解:在![]() 中,
中,![]() ,
,
∴![]() ,
,
①当![]() (
(![]() )时,
)时,
![]() ,即
,即![]() ,
,
∴![]() .
.
此时点![]() 的坐标是
的坐标是![]() .
.
②当![]() (
(![]() )时,
)时,
![]() .即
.即![]() ,
,
∴![]() ,
,
![]() ,
,
此时点![]() 的坐标是
的坐标是![]() ;
;
③当![]() (
(![]() )时,点
)时,点![]() 不在
不在![]() 轴上;
轴上;
综上所述,在![]() 轴上存在一点
轴上存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似,点
相似,点![]() 的坐标是
的坐标是![]() 或
或![]() .
.

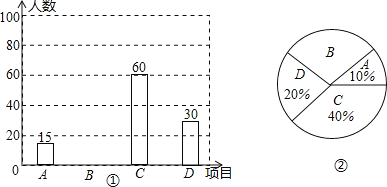
【题目】某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
类别 | 频数(人数) | 频率 |
武术类 | 0.20 | |
书画类 | 15 | 0.l5 |
棋牌类 | 25 |
|
器乐类 | ||
合计 |
| 1.00 |
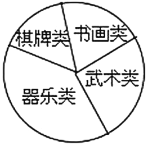
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题:
①![]() ____,
____,![]() _____;
_____;
②在扇形统计图中,器乐类所对应扇形的圆心角是_____度;
③若该校七年级有学生460人,请你估计大约有多少学生参加武术类校本课程.