题目内容
 如图,从台阶的下端点B到上端点A的直线距离为
如图,从台阶的下端点B到上端点A的直线距离为
- A.
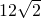
- B.

- C.
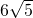
- D.
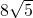
A
分析:将所有的高相加作为新直角三角形的一条直角边,将所有的宽相加作为新直角三角形的另一条直角边,利用勾股定理求得直角三角形的斜边即可求解.
解答: 解:根据题意得:AC=2+8+2=12,BC=4+4+4=12,
解:根据题意得:AC=2+8+2=12,BC=4+4+4=12,
根据勾股定理得:AB= =
=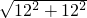 =12
=12 ,
,
故选A.
点评:本题考查了勾股定理的应用,解题的关键是正确的构造直角三角形.
分析:将所有的高相加作为新直角三角形的一条直角边,将所有的宽相加作为新直角三角形的另一条直角边,利用勾股定理求得直角三角形的斜边即可求解.
解答:
 解:根据题意得:AC=2+8+2=12,BC=4+4+4=12,
解:根据题意得:AC=2+8+2=12,BC=4+4+4=12,根据勾股定理得:AB=
 =
=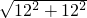 =12
=12 ,
,故选A.
点评:本题考查了勾股定理的应用,解题的关键是正确的构造直角三角形.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
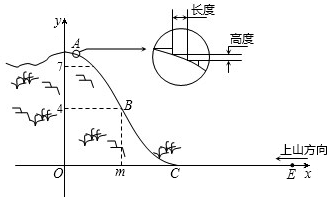 试求索道的最大悬空高度.
试求索道的最大悬空高度. 如图,从台阶的下端点B到上端点A的直线距离为( )
如图,从台阶的下端点B到上端点A的直线距离为( )




