题目内容
 (2013•莒南县二模)已知直线y=2x+2与x轴、y轴交于A、B两点,过点C(2,0)作直线AB的垂线,垂足为D.
(2013•莒南县二模)已知直线y=2x+2与x轴、y轴交于A、B两点,过点C(2,0)作直线AB的垂线,垂足为D.(1)求直线CD的解析式;
(2)求点C到直线AB的距离;
(3)推广:若已知直线y=k1x+b1和直线y=k2x+b2互相垂直,请猜想直线常数k1、k2之间的关系.只写出结论,无需证明.
分析:(1)如图直线AB的函数解析式为y=2x+2,即tan∠1=2,与直线AB垂直的直线CD的函数解析式为y=kx+b,即tan(180°-∠2)=k,所以利用正切三角函数的定义求得k的值,且C(2,0)代入方程,即可得出.
(2)由(1)的解答过程可以得到CD的长度;
(3)根据(1)中的两直线的函数表达式,得出k1•k2的值.
(2)由(1)的解答过程可以得到CD的长度;
(3)根据(1)中的两直线的函数表达式,得出k1•k2的值.
解答: 解:(1)如图,∵直线AB的解析式为y=2x+2,
解:(1)如图,∵直线AB的解析式为y=2x+2,
∴易求A(-1,0),B(0,2),
∴OA=1,OB=2,
∴在直角△AOB中,tan∠1=
=2.即OB=2OA.
∵AB⊥CD,
∴tan∠1=
=2,
∴tan∠2=
=
,
∴tan(180°-∠2)=-tan∠2=-
.
故设直线CD的解析式为:y=-
x+b.
又∵C(2,0),
∴0=-
×2+b.
解得,b=1,
则直线CD的解析式为:y=-
x+1;
(2)由(1)知,tan∠1=
=2,即CD=2AD,AC=3.
则在直角△ACD中,AC2=AD2+CD2,即9=5AD2,
解得,AD=
,
则CD=2AD=
;
(3)k1•k2=-1.理由如下:
由(1)知,由图中图象得到直线AB的函数表达式y=2x+2,直线CD的函数表达式y=-
x+1
则k1•k2=2×(-
)=-1.
 解:(1)如图,∵直线AB的解析式为y=2x+2,
解:(1)如图,∵直线AB的解析式为y=2x+2,∴易求A(-1,0),B(0,2),
∴OA=1,OB=2,
∴在直角△AOB中,tan∠1=
| OB |
| OA |
∵AB⊥CD,
∴tan∠1=
| CD |
| AD |
∴tan∠2=
| AD |
| DC |
| 1 |
| 2 |
∴tan(180°-∠2)=-tan∠2=-
| 1 |
| 2 |
故设直线CD的解析式为:y=-
| 1 |
| 2 |
又∵C(2,0),
∴0=-
| 1 |
| 2 |
解得,b=1,
则直线CD的解析式为:y=-
| 1 |
| 2 |
(2)由(1)知,tan∠1=
| CD |
| AD |
则在直角△ACD中,AC2=AD2+CD2,即9=5AD2,
解得,AD=
3
| ||
| 5 |
则CD=2AD=
6
| ||
| 5 |
(3)k1•k2=-1.理由如下:
由(1)知,由图中图象得到直线AB的函数表达式y=2x+2,直线CD的函数表达式y=-
| 1 |
| 2 |
则k1•k2=2×(-
| 1 |
| 2 |
点评:本题考查了一次函数综合题.熟记一次函数图象与几何变换.互相垂直的两条直线的斜率的乘积等于-1.

练习册系列答案
相关题目
 (2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE.
(2013•莒南县二模)如图,在⊙O中,OA、OB是半径,且OA⊥OB,OA=6,点C是AB上异于A、B的动点.过点C作CD⊥OA于点D,作CE⊥OB于点E,连接DE,点G、H在线段DE上,且DG=GH=HE. (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: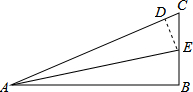 (2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )
(2013•莒南县二模)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点D落在AC边上,折痕为AE,则BE的长为( )