题目内容
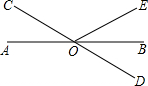
 如图,AB、CD相交于点O,∠1=82°,如果DE∥AB,那么∠D的度数为
如图,AB、CD相交于点O,∠1=82°,如果DE∥AB,那么∠D的度数为
- A.88°
- B.98°
- C.108°
- D.118°
B
分析:先根据对顶角相等求出∠2,再根据两直线平行,同旁内角互补列式计算即可得解.
解答: 解:∵∠1=82°,
解:∵∠1=82°,
∴∠2=∠1=82°,
∵DE∥AB,
∴∠D=180°-∠2=180°-82°=98°.
故选B.
点评:本题主要考查了两直线平行,同旁内角互补的性质,对顶角相等的性质,熟记性质是解题的关键.
分析:先根据对顶角相等求出∠2,再根据两直线平行,同旁内角互补列式计算即可得解.
解答:
 解:∵∠1=82°,
解:∵∠1=82°,∴∠2=∠1=82°,
∵DE∥AB,
∴∠D=180°-∠2=180°-82°=98°.
故选B.
点评:本题主要考查了两直线平行,同旁内角互补的性质,对顶角相等的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
 如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是
如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是 如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是
如图,AB与CD相交于点O,AD∥BC,AD:BC=1:3,AB=10,则AO的长是 如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC=
如图,AB与CD相交于点O,OA=3,OB=5,0D=6.当OC= (2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
(2009•同安区模拟)已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点. 已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.
已知:如图直线AB、CD相交于点O,OE平分∠AOD,∠FOC=90°,∠1=30°.求∠2和∠3的度数.