题目内容
 如图所示,⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,且sin∠CBD=
如图所示,⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,且sin∠CBD= ,则OM=
,则OM=
- A.

- B.

- C.1
- D.

A
分析:连接AO并延长交⊙O于点E,连接BE,则∠ABE=90°,由于BD⊥AC,所以∠BDC=90°,由于∠AEB=∠ACB,所以∠BAE=∠CBD,故sin∠BAE=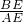 =sin∠CBD=
=sin∠CBD= ,故可求出BE的长,再根据O是AE的中点,OM⊥AM可知OM是△ABE的中位线,故OM=
,故可求出BE的长,再根据O是AE的中点,OM⊥AM可知OM是△ABE的中位线,故OM= BE,故可得出结论.
BE,故可得出结论.
解答: 解:连接AO并延长交⊙O于点E,连接BE,
解:连接AO并延长交⊙O于点E,连接BE,
∵AE是⊙O的直径,⊙O的半径为2,
∴∠ABE=90°,AE=4,
∵BD⊥AC,
∴∠BDC=90°,
∵∠AEB=∠ACB,
∴∠BAE=∠CBD,
∴sin∠BAE=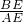 =sin∠CBD=
=sin∠CBD= =
=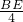 ,解得BE=1,
,解得BE=1,
∵O是AE的中点,OM⊥AM,
∴OM是△ABE的中位线,
∴OM= BE=
BE= .
.
故选A.
点评:本题考查的是圆周角定理及三角形的中位线定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
分析:连接AO并延长交⊙O于点E,连接BE,则∠ABE=90°,由于BD⊥AC,所以∠BDC=90°,由于∠AEB=∠ACB,所以∠BAE=∠CBD,故sin∠BAE=
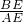 =sin∠CBD=
=sin∠CBD= ,故可求出BE的长,再根据O是AE的中点,OM⊥AM可知OM是△ABE的中位线,故OM=
,故可求出BE的长,再根据O是AE的中点,OM⊥AM可知OM是△ABE的中位线,故OM= BE,故可得出结论.
BE,故可得出结论.解答:
 解:连接AO并延长交⊙O于点E,连接BE,
解:连接AO并延长交⊙O于点E,连接BE,∵AE是⊙O的直径,⊙O的半径为2,
∴∠ABE=90°,AE=4,
∵BD⊥AC,
∴∠BDC=90°,
∵∠AEB=∠ACB,
∴∠BAE=∠CBD,
∴sin∠BAE=
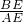 =sin∠CBD=
=sin∠CBD= =
=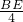 ,解得BE=1,
,解得BE=1,∵O是AE的中点,OM⊥AM,
∴OM是△ABE的中位线,
∴OM=
 BE=
BE= .
.故选A.
点评:本题考查的是圆周角定理及三角形的中位线定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
 37、如图所示,⊙O的半径为5,点P为⊙O外一点,OP=8cm.
37、如图所示,⊙O的半径为5,点P为⊙O外一点,OP=8cm.
 如图所示,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移
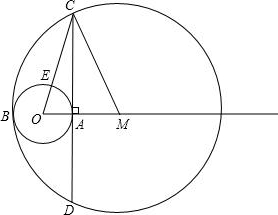
如图所示,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移 如图所示,⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,且sin∠CBD=
如图所示,⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,且sin∠CBD=