题目内容
已知:如图, 中,
中, ,
, 于
于 ,
, 平分
平分 ,
,
且 于
于 ,与
,与 相交于点
相交于点 是
是 边的中点,
边的中点,
连结 与
与 相交于点
相交于点 .
.
(1)判断AC与图中的那条线段相等,并证明你的结论;
(2)若 的长为
的长为 ,求BG的长.
,求BG的长.

(1)证明: ,∴
,∴ ,
,
∵ ,
,

 是等腰直角三角形.
是等腰直角三角形.
 .………..…………………2分
.………..…………………2分
∵ 于
于 ,∴
,∴ ,
,
∵ ,
, .
.
 .
.
 .………..…………………3分
.………..…………………3分
(2)解: 平分
平分 ,
, .
.
∵ 于
于 ,∴
,∴ ,
,
又∵BE=BE, .
.
 .………..…………………4分
.………..…………………4分
连结 .
. 是等腰直角三角形,
是等腰直角三角形, .
.
又 是
是 边的中点,
边的中点,
 垂直平分
垂直平分 ,
, .
.
 ,
,
∴ ,∴
,∴ 是等腰直角三角形,
是等腰直角三角形,
∵ 的长为
的长为 ,∴EG=
,∴EG= ,
,
利用勾股定理得: ,∴
,∴ ,
,
∴ ,∴BG的长为
,∴BG的长为 .………..…………………6分
.………..…………………6分

练习册系列答案
相关题目

 .
. D.
D.
 ,则 a 的取值范围是( ) A.
,则 a 的取值范围是( ) A.  B.
B.  C.
C.  D.
D.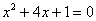 .
.