题目内容
巴蜀中学2017春季运动会的开幕式精彩纷呈,主要分为以下几个类型:A文艺范、B动漫潮、C学院派、D民族风,为了解未能参加运动会的初三学子对开幕式类型的喜好情况,学生处在初三年级随机抽取了一部分学生进行调查,并将他们喜欢的种类绘制成如下统计图,请你根据统计图解答以下问题:
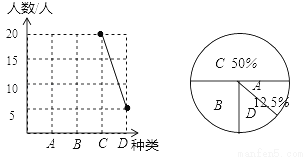
(1)请补全折线统计图,并求出“动漫潮”所在扇形的圆心角度数.
(2)据统计,在被调查的学生中,喜欢“文艺范”类型的仅有2名住读生,其余均为走读生,初二年级欲从喜欢“文艺范”的这几名同学中随机抽取两名同学去观摩“文明礼仪大赛”视频,用列表法或树状图的方法求出所选的两名同学都是走读生的概率.
(1)90°;(2). 【解析】试题分析:(1)根据等级C的人数除以占的百分比求出调查的学生数,进而确定出等级A的人数即可;补全统计图即可; (2)列表得出所有等可能的情况数,找出所选两位同学恰好都是走读生的情况数,即可求出所求的概率. 试题解析:【解析】 (1)被调查的学生数为;20÷50%=40人,A文艺范人数=40×12.5%=5人,B动漫潮人数=40﹣5﹣5﹣20=10...
练习册系列答案
相关题目


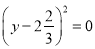 ,那么x﹣y=_____.
,那么x﹣y=_____.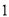 ,在
,在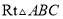 中,
中, 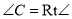 ,
, 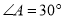 ,
, 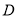 为
为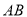 上一个动点,过点
上一个动点,过点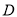 作
作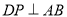 交折线
交折线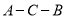 于点
于点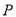 ,设
,设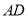 的长为
的长为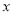 ,
, 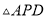 的面积为
的面积为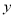 ,
, 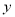 关于
关于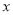 函数图象
函数图象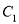 ,
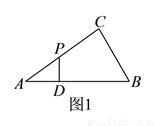
, 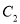 两段组成,如图
两段组成,如图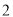 所示.
所示. )当
)当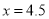 时,求
时,求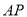 的长.
的长.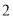 )求图
)求图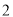 中的图象
中的图象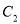 段的函数解析式.
段的函数解析式.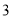 )求
)求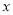 为何值时,
为何值时, 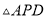 的面积为
的面积为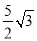 .
.
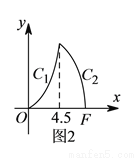
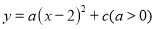 ,当自变量
,当自变量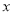 分别取
分别取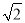 、
、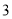 、
、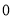 时,对应的函数值分别:
时,对应的函数值分别: 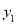 ,
, 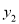 ,
, 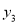 ,则
,则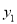 ,
, 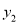 ,
, 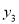 的大小关系正确的是( ).
的大小关系正确的是( ).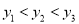 B.
B. 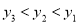 C.
C. 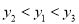 D.
D. 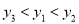
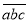 (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 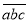 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.