题目内容
2.如图1,△ABC和△DEF是两块可以完全重合的三角板,∠BAC=∠DEF=90°,∠ABC=∠DEF=30°.在图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.(1)当△ABC移到图2位置时,连解AF、DC,求证:AF=DC;
(2)若EF=8,在上述平移过程中,试问点C距点E多远时,线段AD被直线a垂直平分?并证明你的猜想.
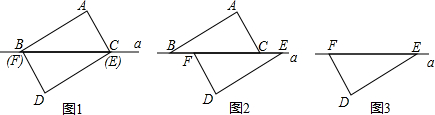
分析 (1)连接AF,CD,由BC=EF,得到BF=CE,证明△ABF≌△DEC,得到AF=DC.
(2)当点C距点E的距离为4时,线段AD被直线a垂直平分,利用直角三角形的性质,进行解答即可.
解答 解:(1)如图2,连接AF,CD,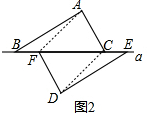
∵BC=EF,
∴BC-FC=EF-FC,
即BF=CE,
在△ABF和△DEC中,
$\left\{\begin{array}{l}{AB=DE}\\{∠ABF=∠DEF}\\{BF=EC}\end{array}\right.$,
∴△ABF≌△DEC,
∴AF=DC.
(2)当点C距点E的距离为4时,线段AD被直线a垂直平分,
证明:如图3,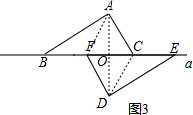
∵AF=DC,AC=DF,
∴四边形AFDC是平行四边形,
若AD被直线a垂直平分,假设a与AD交于点O,
在Rt△EFD中,∠DEF=30°
∴DF=$\frac{1}{2}$EF=4,
在Rt△FDO中,∠FDO=30°,
∴OF=$\frac{1}{2}$DF=2,
∴OC=2,
∴CE=EF-OF-OC=8-2-2=4.
点评 本题考查了全等三角形的性质与判定,直角三角形的性质,解决本题的关键是证明△ABF≌△DEC.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
12.下列各式中计算错误的是( )
| A. | 2x(2x3+3x-1)=4x4+6x2-2x | B. | b(b2-b+1)=b3-b2+b | ||
| C. | -$\frac{1}{2}x(2{x^2}-2)=-{x^3}$-x | D. | $\frac{2}{3}x(\frac{3}{2}{x^3}-3x+1)={x^4}-2{x^2}+\frac{2}{3}$x |
 如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为40°.
如图,△ABC和△BDE都是等边三角形,如果∠ABE=40°.那么∠CBD的大小为40°.
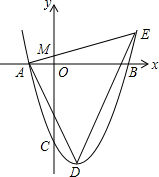 如图.抛物线y=x2一2x-8与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,E为第一象限的抛物线上一点.且DE为△ADE的外接圆的直径,AD交y轴于F.
如图.抛物线y=x2一2x-8与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点,E为第一象限的抛物线上一点.且DE为△ADE的外接圆的直径,AD交y轴于F.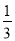 )-2-(-1)2016-
)-2-(-1)2016-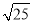 +(π-1)0
+(π-1)0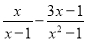
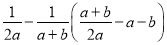
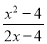 的值为零,则x等于( )
的值为零,则x等于( )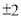 D. 0
D. 0