题目内容
已知△ABC的两条高CD,BE交于点G,外角平分线BF,CF交于点F,
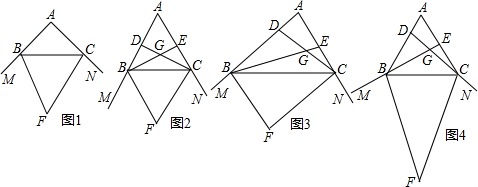
(1)如图1,若△ABC是直角三角形,∠A=90°,那么∠F等于多少度?如图2,若△ABC是等边三角形,那么∠BGC等于多少度?∠F等于多少度?
(2)如图3,若∠A为锐角且∠A=α°,那么∠BGC等于多少?∠F等于多少?由此以上结论猜想∠BGC与∠F的关系?写出你的结论(不必证明)
(3)如图4,若∠A为钝角,那么∠BGC与∠F的关系是否发生改变,若不变请证明,若改变请写出你的结论并证明.

(1)如图1,若△ABC是直角三角形,∠A=90°,那么∠F等于多少度?如图2,若△ABC是等边三角形,那么∠BGC等于多少度?∠F等于多少度?
(2)如图3,若∠A为锐角且∠A=α°,那么∠BGC等于多少?∠F等于多少?由此以上结论猜想∠BGC与∠F的关系?写出你的结论(不必证明)
(3)如图4,若∠A为钝角,那么∠BGC与∠F的关系是否发生改变,若不变请证明,若改变请写出你的结论并证明.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)若△ABC是直角三角形根据三角形外角的性质,求得∠F=90°-
∠A,即可求得∠F的值;若△ABC是等边三角形,根据三角形外角的性质,求得∠F=90°-
∠A=60°根据四边形的内角和等于360°,得出∠DGE=180°-∠A=120°;
(2)根据三角形外角的性质,求得∠F=90°-
∠A,根据四边形的内角和等于360°,得出∠DGE=180°-∠A,因为∠A=α,即可求得∠BGC,∠F的度数;
(3)若∠A为钝角,那么∠BGC与∠F的关系不会发生改变,可根据三角形外角的性质,求得∠F=90°-
∠BAC,根据四边形的内角和等于360°,得出∠BGC=180°-DAE=180°-∠BAC,所以∠BGC=2∠F.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据三角形外角的性质,求得∠F=90°-
| 1 |
| 2 |
(3)若∠A为钝角,那么∠BGC与∠F的关系不会发生改变,可根据三角形外角的性质,求得∠F=90°-
| 1 |
| 2 |
解答:解:(1)如图1,∵外角平分线BF,CF交于点F,
∴∠CBF=
∠MBC=
(∠A+∠ACB),∠BCF=
(∠A+∠ABC)
∵∠F=180°-(∠CBF+∠BCF)=180°-(∠A+
∠ACB+
∠ABC)=180°-∠A-
(180°-∠A)=90°-
∠A,
∵∠A=90°,
∴∠F=45°,
如图2,∵△ABC是等边三角形,
∴∠A=60°
∵CD,BE是△ABC的两条高,
∴∠DGE=180°-∠A=120°,
∴∠BGC=120°,
∵△ABC是等边三角形,
∴∠MBC=∠NCB=120°,
∴外角平分线BF,CF交于点F,
∴∠FBC=∠BCF=60°,
∴∠F=60°,
(2)如图3,∵△ABC的两条高CD,BE交于点G,∠A=α°,
∴∠BGC=∠DGE=180°-α,
∵∠F=180°-(∠CBF+∠BCF)=180°-(∠A+
∠ACB+
∠ABC)=180°-∠A-
(180°-∠A)=90°-
∠A,
∴∠F=90°-
α,
由此以上结论猜想∠BGC与∠F的关系为:∠BGC=2∠F;
(3)如图4,若∠A为钝角,那么∠BGC与∠F的关系不发生改变,仍是∠BGC=2∠F;
理由:∵△ABC的两条高CD,BE交于点G,
∴∠BGC=180°-DAE=180°-∠BAC,
∵外角平分线BF,CF交于点F,
∴∠CBF=
∠MBC=
(∠BAC+∠ACB),∠BCF=
(∠BAC+∠ABC)
∵∠F=180°-(∠CBF+∠BCF)=180°-(∠BAC+
∠ACB+
∠ABC)=180°-∠BAC-
(180°-∠BAC)=90°-
∠BAC,
∴∠BGC=2∠F;
∴∠CBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠F=180°-(∠CBF+∠BCF)=180°-(∠A+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠A=90°,
∴∠F=45°,
如图2,∵△ABC是等边三角形,
∴∠A=60°
∵CD,BE是△ABC的两条高,
∴∠DGE=180°-∠A=120°,
∴∠BGC=120°,
∵△ABC是等边三角形,
∴∠MBC=∠NCB=120°,
∴外角平分线BF,CF交于点F,
∴∠FBC=∠BCF=60°,
∴∠F=60°,
(2)如图3,∵△ABC的两条高CD,BE交于点G,∠A=α°,
∴∠BGC=∠DGE=180°-α,
∵∠F=180°-(∠CBF+∠BCF)=180°-(∠A+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠F=90°-
| 1 |
| 2 |
由此以上结论猜想∠BGC与∠F的关系为:∠BGC=2∠F;
(3)如图4,若∠A为钝角,那么∠BGC与∠F的关系不发生改变,仍是∠BGC=2∠F;
理由:∵△ABC的两条高CD,BE交于点G,
∴∠BGC=180°-DAE=180°-∠BAC,
∵外角平分线BF,CF交于点F,
∴∠CBF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠F=180°-(∠CBF+∠BCF)=180°-(∠BAC+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BGC=2∠F;
点评:本题考查了三角形的内角和定理,四边形内角和定理,三角形的外角的性质等,熟练掌握性质和定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知:如图,三角形ABC
已知:如图,三角形ABC