题目内容
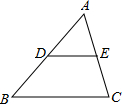附加题：如图，在△ABC中，BC=2，则中位线DE=分析：根据三角形的中位线平行于第三边并且等于第三边的一半求解．
解答：解：在△ABC中，
∵BC=2，
∴中位线DE=
BC=1．
∵BC=2，
∴中位线DE=
| 1 |
| 2 |
点评：本题主要考查三角形的中位线定理，三角形中位线的性质为我们证明两直线平行，两条线段之间的数量关系又提供了一个重要的依据．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
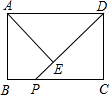附加题：如图，在矩形ABCD中，AB=3，BC=4，点P在BC边上运动，连接DP，过点A作AE⊥DP，垂足为E，设DP=x，AE=y，则能反映y与x之间函数关系的大致图象是（ ）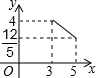
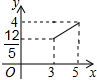
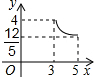
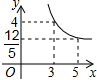
27、附加题：
附加题：
（附加题）如图，在一块三角形区域土地ABC中，∠C=90°，AC=8，BC=6，底边AB上的高h=