Question

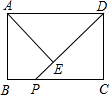附加题：如图，在矩形ABCD中，AB=3，BC=4，点P在BC边上运动，连接DP，过点A作AE⊥DP，垂足为E，设DP=x，AE=y，则能反映y与x之间函数关系的大致图象是（　　）

• A、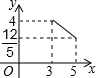
• B、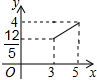
• C、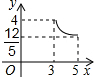
• D、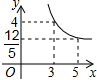

Answer 1

分析：根据实际情况求得自变量的取值范围．

解答：解：
∵S_△APD=

1

2

PD×AE=

1

2

AD×AB，
∴xy=3×4
∴xy=12，
即：y=

12

x

，为反比例函数，
当P点与C点重合时，x为最小值：x=3，
当P点与B点重合时，x为最大值：x=BD=

32+42

=5，
∴3≤x≤5．
故选：C．

点评：本题考查了动点问题的函数图象，解决本题的关键是利用相似求得y与x的函数关系式，特别是要确定自变量的取值范围．