题目内容
已知：如图，点D是AB的中点，
，DC=1，求AB的长．
解：∵BC=
AB，
∴设BC=x，则AB=3x，
∵点D是AB的中点，
∴DB=
AB=
x，
∵DB-CB=DC，DC=1，
∴x-x=1，
∴x=2，
∴AB=3x=6．
另解：∵BC=AB，
∴设AB=x，则BC=x，
∵点D是AB的中点，
∴DB=AB=x，
∵DB-CB=DC，DC=1，
∴x-x=1，
∴x=6，
∴AB=6．
分析：先根据BC=AB，设BC=x，则AB=3x，由点D是AB的中点可知DB=AB=x，再根据DB-CB=DC，DC=1，可得出x-x=1，故可得出x的值，进而得出结论．
点评：本题考查的是两点间的距离，熟知各线段之间的和、差及倍数关系是解答此题的关键．
AB，∴设BC=x，则AB=3x，
∵点D是AB的中点，
∴DB=
AB=x，∵DB-CB=DC，DC=1，
∴
x-x=1，∴x=2，
∴AB=3x=6．
另解：∵BC=
AB，∴设AB=x，则BC=
x，∵点D是AB的中点，
∴DB=
AB=x，∵DB-CB=DC，DC=1，
∴
x-x=1，∴x=6，
∴AB=6．
分析：先根据BC=
AB，设BC=x，则AB=3x，由点D是AB的中点可知DB=AB=x，再根据DB-CB=DC，DC=1，可得出x-x=1，故可得出x的值，进而得出结论．点评：本题考查的是两点间的距离，熟知各线段之间的和、差及倍数关系是解答此题的关键．
练习册系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
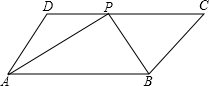BA．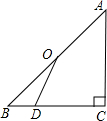
已知：如图，点O是等腰直角△ABC斜边AB的中点，D为BC边上任意一点．
10、已知：如图，点P是正方形ABCD的对角线AC上的一个动点（A、C除外），作PE⊥AB于点E，作PF⊥BC于点F，设正方形ABCD的边长为x，矩形PEBF的周长为y，在下列图象中，大致表示y与x之间的函数关系的是（ ）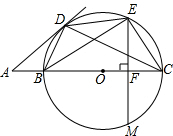
B=∠DEB，EF⊥BC于点F，交⊙O于点M，EM=2
25、已知：如图，点D是△ABC的边AC上的一点，过点D作DE⊥AB，DF⊥BC，E、F为垂足，再过点D作DG∥AB，交BC于点G，且DE=DF．