Question

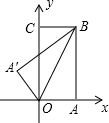如图，把一矩形纸片OABC放入平面直角坐标系xoy中，使OA、OC分别落在x轴、y轴上，现将纸片OABC沿OB折叠，折叠后点A落在点A'的位置，若OA=1，OB=2，则点A'的坐标为（　　）

• A、( 

  1

  2

  ，

  3

  2

   )
• B、( -

  1

  2

  ， 

  3

  2

   )
• C、（-

  3

  5

  ， 

  4

  5

  ）
• D、（-

  3

  ，  1）

Answer 1

分析：在直角△OAB中利用三角函数即可求得∠BOA的度数，进而求得∠A′OD的度数，在直角△A′OD中利用三角函数即可求得OD，A′D的长度，从而求得A′的坐标．

解答：解：过A′作A′D⊥x轴与点D．
在直角△OAB中，∵cos∠BOA=

OA

OB

=

1

2

∴∠BOA=60°
∴∠A′OB=∠BOA=60°
∴∠A′OD=60°
在直角△A′OD中，OD=OA′•cos60°=1×

1

2

=

1

2

；
A′D=A′O•sin60°=1×

3

2

=

3

2

．
∴点A'的坐标为（-

1

2

，

3

2

）．
故选B．

点评：本题主要考查了三角函数以及图形的折叠，在折叠的过程中要注意不变的量，求点的坐标的问题一般是过点作坐标轴的垂线，转化为求线段的长的问题．