题目内容
根据题意,在横线上写出相应的函数关系式,并判断y是否为x的反比例函数(“是”就在后面的空格内打“1”,“不是”就在后面的空格内打“0”):(1)长方形的面积S(cm2)一定,它的长y(cm)与宽x(cm)之间的关系式为;
(2)正方形的对角线长y(cm)与它的边长x(cm)之间的关系式为;
(3)一种商品的单价为a(元/件),所花费的钱数y(元)与购买的件数x(件)的关系式为;
(4)小明的家与学校相距2 400m,他骑自行车上学的速度v(m/s)与所需时间t(s)的关系式为..
分析:(1)长方形的长=面积÷宽,面积一定,故长与宽是反比例函数关系;
(2)根据勾股定理可得:正方形的对角线长2=2边长2,∴正方形的对角线长=
边长,常数是
,不是反比例函数;
(3)总价=单价×数量,单价一定,不是反比例函数;
(4)速度=路程÷时间,路程一定,是反比例函数.
(2)根据勾股定理可得:正方形的对角线长2=2边长2,∴正方形的对角线长=
| 2 |
| 2 |
(3)总价=单价×数量,单价一定,不是反比例函数;
(4)速度=路程÷时间,路程一定,是反比例函数.
解答:解:(1)由题意得:y=
,是反比例关系;
(2)由题意得:y=
x(x>0),不是反比例关系;
(3)由题意得:y=ax,不是反比例关系;
(4)由题意得:y=
,是反比例关系.
故本题答案为:(1)y=
,1;(2)y=
x(x>0),0;(3)y=ax,0;(4)y=
,1.
| S |
| x |
(2)由题意得:y=
| 2 |
(3)由题意得:y=ax,不是反比例关系;
(4)由题意得:y=
| 2400 |
| t |
故本题答案为:(1)y=
| S |
| x |
| 2 |
| 2400 |
| t |
点评:根据题意,找到所求量的等量关系是解决问题的关键.除法一般写成分式的形式,除号可看成分式线,反比例函数的一般形式是y=
(k为常数,且k≠0).
| k |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
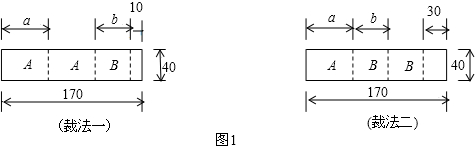
(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个.(在横线上直接写出答案,无需书写过程)

(1)列出方程(组),求出图甲中a与b的值.
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
| 礼品盒板 材 | 竖式无盖(个) | 横式无盖(个) |
| x | y | |
| A型(张) | 4x | 3y |
| B型(张) | x |

③做成的竖式和横式两种无盖礼品盒总数最多是

 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的