题目内容
 如图边长为a的正方形ABCD沿直线l向右滚动.当正方形滚动一周时,正方形中心O经过的路程为
如图边长为a的正方形ABCD沿直线l向右滚动.当正方形滚动一周时,正方形中心O经过的路程为| 2 |
| 2 |
(1+
)πa
| ||
| 2 |
(1+
)πa
.
| ||
| 2 |
分析:要计算正方形滚动一周时,正方形中心O和顶点A所走的路程,就必须弄清它们的运动过程:
中心O:当正方形滚动一周时,中心O所经过的路程为4段弧,且都是以90°为圆心角、对角线的一半为半径,因此中心O实际经过的路程是一个圆,且半径为对角线的一半,由此得解;点A:当正方形滚动一周时,点A也经过了4段弧,可分作两部分:
一、以90°为圆心角、对角线长为半径的两段弧,二、以90°为圆心角、边长长为半径的两段弧;可根据弧长计算公式进行求解即可.
中心O:当正方形滚动一周时,中心O所经过的路程为4段弧,且都是以90°为圆心角、对角线的一半为半径,因此中心O实际经过的路程是一个圆,且半径为对角线的一半,由此得解;点A:当正方形滚动一周时,点A也经过了4段弧,可分作两部分:
一、以90°为圆心角、对角线长为半径的两段弧,二、以90°为圆心角、边长长为半径的两段弧;可根据弧长计算公式进行求解即可.
解答: 解:根据勾股定理可得:AC=
解:根据勾股定理可得:AC=
a,即OC=
a,
正方形中心O经过的路程=
=
aπ,
点A经过的路程=
+
=(1+
)πa.
故答案为:
aπ,(1+
)πa.
 解:根据勾股定理可得:AC=
解:根据勾股定理可得:AC=| 2 |
| ||
| 2 |
正方形中心O经过的路程=
90π×
| ||||
| 180 |
| 2 |
点A经过的路程=
90π×
| ||
| 180 |
| 90π×a×2 |
| 180 |
| ||
| 2 |
故答案为:
| 2 |
| ||
| 2 |
点评:此题主要考查了弧长的计算方法以及锐角三角函数的定义,能够发现正方形滚动过程中,中心和顶点的移动轨迹是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
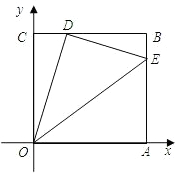 轴上.动点D在线段BC上移动(不与B、C重合),连接OD,过点D作DE⊥OD,交边AB于点E,记CD的长为t.
轴上.动点D在线段BC上移动(不与B、C重合),连接OD,过点D作DE⊥OD,交边AB于点E,记CD的长为t.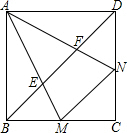 已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°
已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45° 已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为( )
已知,如图边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为( )
