题目内容
3.生产某产品要经过三道工序.同一个人在完成这三道工序时所用的时间相同.甲、乙二人同时开始生产,一段时间后,甲恰好完成第k个产品的生产,此时,乙正好在进行某个产品的第一道工序的操作.若甲、乙的生产效率比是6:5.则此时乙至少生产了多少产品?分析 设出甲生产一个产品所用的时间为t,得出乙生产一个产品所用的时间为$\frac{6}{5}$t. 进而得出甲生产k个产品时乙生产的产品数量的范围,再找规律得出满足以0<{$\frac{5k}{6}$}<$\frac{1}{3}$的最小的k的值是5,即可得出结论.
解答 解:设甲生产一个产品所用的时间为t,则乙生产一个产品所用的时间为$\frac{6}{5}$t.
用[a]表示不大于a的最大整数,{a}=a-[a],如[3.14]=3,{3.14}=0.14,
甲生产k个产品所用的时间为kt,此时乙生产了[$\frac{kt}{\frac{6}{5}t}$]=[$\frac{5k}{6}$]个产品
由题知,乙正在进行某个产品的第一道工序的操作,
所以 0<{$\frac{5k}{6}$}<$\frac{1}{3}$,
∴{$\frac{5k}{6}$}的可能取值为:$\frac{1}{6}$,$\frac{1}{3}$,$\frac{1}{2}$,$\frac{2}{3}$,$\frac{5}{6}$,0,
当k=1时,{$\frac{5k}{6}$}的值为$\frac{5}{6}$,当k=2时,{$\frac{5k}{6}$}的值为$\frac{2}{3}$,当k=3时,{$\frac{5k}{6}$}的值为$\frac{1}{2}$,
当k=4时,{$\frac{5k}{6}$}的值为$\frac{1}{3}$,当k=5时,{$\frac{5k}{6}$}的值为$\frac{1}{6}$,当k=6时,{$\frac{5k}{6}$}的值为0,
当k=7时,{$\frac{5k}{6}$}的值为$\frac{5}{6}$,当k=8时,{$\frac{5k}{6}$}的值为$\frac{2}{3}$,当k=时9,{$\frac{5k}{6}$}的值为$\frac{1}{2}$,
当k=10时,{$\frac{5k}{6}$}的值为$\frac{1}{3}$,当k=11时,{$\frac{5k}{6}$}的值为$\frac{1}{6}$,当k=12时,{$\frac{5k}{6}$}的值为0,?
…
由以上数据得出,满足以0<{$\frac{5k}{6}$}<$\frac{1}{3}$的最小的k的值是5,
因此,乙至少已经生产了[$\frac{5×5}{6}$]=4个产品.
点评 此题是推理与论证的题目,主要考查了一个数的不大于它的最大整数的确定,寻找规律,解本题的关键是确定出0<{$\frac{5k}{6}$}<$\frac{1}{3}$.是一道很好的推理题目.

| 项目 品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
| A | 800 | x | 800x |
| B | 1000 | 120-x | 1000(120-x) |
①$\frac{π}{2}$是分数;
②绝对值等于本身的数是0.1;
③任何无理数都是无限小数;
④近似数7.30所表示的准确数a的范围是:7.295≤a<7.305
其中正确的项数有( )
| A. | 1项 | B. | 2项 | C. | 3项 | D. | 4项 |
| A. | x2+2xy+4y2 | B. | 25m2+10mn+n2 | C. | a2+ab+b2 | D. | x2-2xy-$\frac{1}{4}$y2 |
| A. | 1 | B. | -1 | C. | 2012 | D. | -2012 |
 按下列要求作图并解答:
按下列要求作图并解答: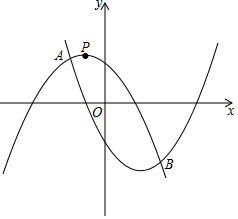 如图所示,抛物线y1=-ax2+(a-1)x+1经过点P(-$\frac{1}{3}$,$\frac{10}{9}$),且与抛物线y2=ax2-(a+1)x-1相交于A,B两点.
如图所示,抛物线y1=-ax2+(a-1)x+1经过点P(-$\frac{1}{3}$,$\frac{10}{9}$),且与抛物线y2=ax2-(a+1)x-1相交于A,B两点.