题目内容
10.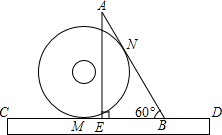 小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是$\frac{4\sqrt{3}}{3}$.
小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上,此时,光盘与AB,CD分别相切于点N,M.现从如图所示的位置开始,将光盘在直尺边上沿着CD向右滚动到再次与AB相切时,光盘的圆心经过的距离是$\frac{4\sqrt{3}}{3}$.
分析 根据切线的性质得到OH=PH,根据锐角三角函数求出PH的长,得到答案.
解答  解:如图,当圆心O移动到点P的位置时,光盘在直尺边上沿着CD向右滚动到再次与AB相切,切点为Q,
解:如图,当圆心O移动到点P的位置时,光盘在直尺边上沿着CD向右滚动到再次与AB相切,切点为Q,
∵ON⊥AB,PQ⊥AB,
∴ON∥PQ,
∵ON=PQ,∴OH=PH,
在Rt△PHQ中,∠P=∠A=30°,PQ=1,
∴PH=$\frac{2\sqrt{3}}{3}$,
则OP=$\frac{4\sqrt{3}}{3}$,
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查的是直线与圆相切的知识,掌握圆的切线垂直于过切点的半径是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.计算:-3+4的结果等于( )
| A. | 7 | B. | -7 | C. | 1 | D. | -1 |
5.若式子$\sqrt{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≥0 |
 已知:在等腰Rt△ABC中,AC=BC,∠C=90°,AD平分∠BAC,DE⊥AB于点E.求证:BD+DE=AC.
已知:在等腰Rt△ABC中,AC=BC,∠C=90°,AD平分∠BAC,DE⊥AB于点E.求证:BD+DE=AC.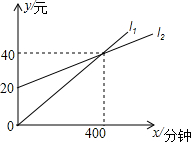 一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论:
一家电信公司提供两种手机的月通话收费方式供用户选择,其中一种有月租费,另一种无月租费.这两种收费方式的通话费用y(元)与通话时间x(分钟)之间的函数关系如图所示.小红根据图象得出下列结论: 小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)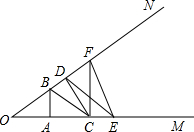 如图,∠MON两边上分别有A,C,E及D,F,B六个点,且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1,则S△CDF=$\frac{3}{4}$.
如图,∠MON两边上分别有A,C,E及D,F,B六个点,且S△OAB=S△ABC=S△BCD=S△CDE=S△DEF=1,则S△CDF=$\frac{3}{4}$.