Question

【题目】数轴上点表示的数为，点表示的数为，点表示的数为，为原点，且满足．

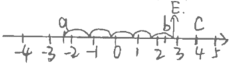
（1）__________，__________，__________；

（2）若的的中点为．则点表示的数为__________；

（3）小亮说“如果将点向右移动5个单位长度，得到点，此时点在原点的右侧，也在点的右侧”，他的说法正确吗？说明理由．

Answer 1

【答案】（1）；5；4；（2）；（3）不正确，理由见解析．

【解析】

（1）根据完全平方式，绝对值及二次根式的非负性求解即可；

（2）利用数轴上两点间的中点公式求解；

（3）利用平移求出E点所表示的数，然后进行实数的大小比较，从而进行判断．

解：（1）由可得

∴

解得：；；

故答案为：；5；4；

（2）由（1）可知：A点表示的数为，C点表示的数为4

∴的的中点表示的数为

故答案为：；

（3）不正确，理由如下：

将点向右移动5个单位长度，得到点，此时点表示的数为+5

∵

∴

又∵点B表示的数为5

∴点E在原点右侧，B点左侧

故小亮说法不正确．