题目内容
11．已知二次函数y=x2-2mx+m2+3（m是常数）．（1）求证：不论m为何值，该函数的图象与x轴没有公共点；
（2）若函数的图象与x轴只有一个公共点，则该把这个函数的图象沿y轴向下平移多少个单位？
分析 （1）求出根的判别式，即可得出答案；
（2）先化成顶点式，根据顶点坐标和平移的性质得出即可．
解答 （1）证明：∵△=（-2m）2-4×1×（m2+3）=4m2-4m2-12=-12＜0，
∴方程x2-2mx+m2+3=0没有实数解，
即不论m为何值，该函数的图象与x轴没有公共点；
（2）解：y=x2-2mx+m2+3=（x-m）2+3，
把函数y=（x-m）2+3的图象沿y轴向下平移3个单位长度后，得到函数y=（x-m）2的图象，它的顶点坐标是（m，0），
因此，这个函数的图象与x轴只有一个公共点，
所以，把函数y=x2-2mx+m2+3的图象沿y轴向下平移3个单位长度后，得到的函数的图象与x轴只有一个公共点．
点评 本题考查了二次函数和x轴的交点问题，根的判别式，平移的性质，二次函数的图象与几何变换的应用，主要考查学生的理解能力和计算能力，题目比较好，有一定的难度．
练习册系列答案
相关题目
1．下列运算正确的是（ ）
| A． | x3•x2=x6 | B． | $（{x^2}{）^{\frac{1}{2}}}=x$ | C． | x0=1 | D． | x5÷x3=x2 |
2．
如图，已知直线a，b被直线c所截，那么∠1的内错角是（ ）
如图，已知直线a，b被直线c所截，那么∠1的内错角是（ ）| A． | ∠2 | B． | ∠3 | C． | ∠4 | D． | ∠5 |
6．
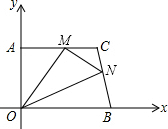在平面直角坐标系中，直角梯形AOBC的位置如图所示，∠OAC=90°，AC∥OB，OA=4，AC=5，OB=6．M、N分别在线段AC、线段BC上运动，当△MON的面积达到最大时，存在一种使得△MON周长最小的情况，则此时点M的坐标为（ ）
在平面直角坐标系中，直角梯形AOBC的位置如图所示，∠OAC=90°，AC∥OB，OA=4，AC=5，OB=6．M、N分别在线段AC、线段BC上运动，当△MON的面积达到最大时，存在一种使得△MON周长最小的情况，则此时点M的坐标为（ ）| A． | （0，4） | B． | （3，4） | C． | （$\frac{5}{2}$，4） | D． | （$\sqrt{3}$，3） |
3．把多项式2x2-18分解因式，结果正确的是（ ）
| A． | 2（x2-9） | B． | 2（x+9）（x-9） | C． | 2（x+3）（x-3） | D． | 2（x-3）2 |
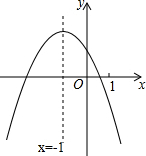二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论：