题目内容
 把一副直角三角板按如图形式叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°.求这副直角三角板重叠部分的面积.
把一副直角三角板按如图形式叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°.求这副直角三角板重叠部分的面积.
分析:首先作出辅助线作EH⊥BC,根据各角度关系得出各边长度,进而求出EH的长度,从而求出即可.
解答: 解:作EH⊥BC于点H,设EH=x.
解:作EH⊥BC于点H,设EH=x.
∵∠ACB=90°,AC=BC=10,
∴∠ABC=45°,
∴BH=EH=x.
∵∠CBD=90°,∠BCD=30°,
∴CH=
x.
∴
x+x=10.
∴x=5(
-1).
∴S△BCE=
×10×5(
-1)=25
-25.
 解:作EH⊥BC于点H,设EH=x.
解:作EH⊥BC于点H,设EH=x.∵∠ACB=90°,AC=BC=10,
∴∠ABC=45°,
∴BH=EH=x.
∵∠CBD=90°,∠BCD=30°,
∴CH=
| 3 |
∴
| 3 |
∴x=5(
| 3 |
∴S△BCE=
| 1 |
| 2 |
| 3 |
| 3 |
点评:此题主要考查了特殊三角形角边关系以及三角形面积求法,根据已知表示出BC的长是解决问题的关键.

练习册系列答案
相关题目

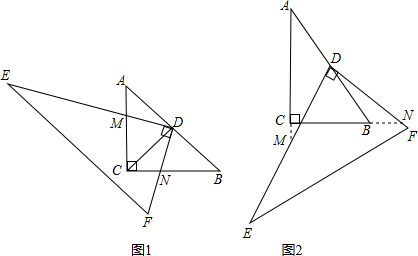
 把一副直角三角板按如图形式叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°.求这副直角三角板重叠部分的面积.
把一副直角三角板按如图形式叠放在一起,其中∠ACB=∠CBD=90°,AC=BC=10,∠BCD=30°.求这副直角三角板重叠部分的面积.