题目内容
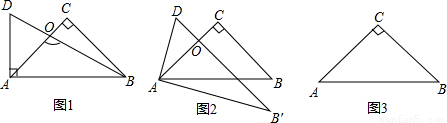
将一副直角三角板按如图1所示方式摆放,其中∠ACB=∠BAD=90°,∠ADB=60°,∠BAC=45°,AC与BD相交于点O.
(1)求∠AOB的度数;
(2)把△ABC固定不动,将△ABD绕着点A顺时针旋转一个大小为α(0°<α<90°)的角,旋转后的点B记为点B′.
①当α为多少度时,∠AOB′为直角?(如图2)
②连接B B′,四边形ACB B′可能为轴对称图形吗?如果可能,请在图3中画出示意图,并求出此时角α的度数;如果不可能,请说明理由.

(1)求∠AOB的度数;
(2)把△ABC固定不动,将△ABD绕着点A顺时针旋转一个大小为α(0°<α<90°)的角,旋转后的点B记为点B′.
①当α为多少度时,∠AOB′为直角?(如图2)
②连接B B′,四边形ACB B′可能为轴对称图形吗?如果可能,请在图3中画出示意图,并求出此时角α的度数;如果不可能,请说明理由.

分析:(1)首先求得∠CBO,然后利用三角形外角的性质求得∠AOB的度数;
(2)若∠AOB′=90°,可以证得:BD∥BC,然后根据平行四边形的性质即可求得;
(3)根据C=CB,因而当△ADB′的点B′旋转到AB的垂直平分线上,那么四边形AB′BC就是轴对称图形.
(2)若∠AOB′=90°,可以证得:BD∥BC,然后根据平行四边形的性质即可求得;
(3)根据C=CB,因而当△ADB′的点B′旋转到AB的垂直平分线上,那么四边形AB′BC就是轴对称图形.
解答: 解:如图1,
解:如图1,
(1)∵∠CBO=45°-30°=15°,∠C=90°,
∴∠AOB=∠CBO+∠C=15°+90°=105°;
(2)如图2,
 ∵∠AOB′=90°,∠C=90°,
∵∠AOB′=90°,∠C=90°,
∴∠AOB′=∠C,
∴BD∥BC,
∴∠AEO=∠B=45°,
∴∠EAB′=∠AEO-∠B′=45°-30°=15°,
∴α=15°;
 (3)当△ADB′的点B′旋转到AB的垂直平分线上,那么四边形AB′BC就是轴对称图形.
(3)当△ADB′的点B′旋转到AB的垂直平分线上,那么四边形AB′BC就是轴对称图形.
∴AB′=BB′=AB,
∴∠BAB′=60°,
∴α=60°.
 解:如图1,
解:如图1,(1)∵∠CBO=45°-30°=15°,∠C=90°,
∴∠AOB=∠CBO+∠C=15°+90°=105°;
(2)如图2,
 ∵∠AOB′=90°,∠C=90°,
∵∠AOB′=90°,∠C=90°,∴∠AOB′=∠C,
∴BD∥BC,
∴∠AEO=∠B=45°,
∴∠EAB′=∠AEO-∠B′=45°-30°=15°,
∴α=15°;
 (3)当△ADB′的点B′旋转到AB的垂直平分线上,那么四边形AB′BC就是轴对称图形.
(3)当△ADB′的点B′旋转到AB的垂直平分线上,那么四边形AB′BC就是轴对称图形.∴AB′=BB′=AB,
∴∠BAB′=60°,
∴α=60°.
点评:本题考查了平行线的性质,以及轴对称图形的性质,正确理解轴对称图形的性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

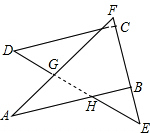 将一副直角三角板按如图放置,使含30°角的三角板的短边与含45°的三角板的一条直角边重合,求∠AGD的度数.
将一副直角三角板按如图放置,使含30°角的三角板的短边与含45°的三角板的一条直角边重合,求∠AGD的度数. 将一副直角三角板按如图放置,使含30°角的三角板的短边与含45°的三角板的一条直角边重合,求∠AGD的度数.
将一副直角三角板按如图放置,使含30°角的三角板的短边与含45°的三角板的一条直角边重合,求∠AGD的度数.