题目内容
在□ABCD中,G为BC延长线上一点,射线AG与直线BD相交于E、与直线CD相交于F.
1.求证:![]() ;
;
2.求证:AE2=EF●EG;
3.如果把“G为BC延长线上一点”改为“G为线段BC上一点(不与点B、C重合)”,其它条件不变,(2)中的结论是否成立吗?若成立,请你加以证明;若不成立,请你说明理由。

1.证明:(1)在□ABCD中,AB∥CD∴∠ABE=∠FDE,∠BAE=∠DFE
∴△ABE∽△FDE∴![]()
2.∵AD∥BC∴∠ADE=∠GBE,∠DAE=∠BGE∴△ADE∽△GBE∴![]()
∴![]() ∴AE2=EF●EG
∴AE2=EF●EG
3.结论AE2=EF●EG成立
证明:在□ABCD中,AB∥CD∴∠ABE=∠FDE,∠BAE=∠DFE∴△ABE∽△FDE∴![]() ∵AD∥BC∴∠ADE=∠GBE,∠DAE=∠BGE∴△ADE∽△GBE∴
∵AD∥BC∴∠ADE=∠GBE,∠DAE=∠BGE∴△ADE∽△GBE∴![]() ∴
∴![]() ∴AE2=EF●EG
∴AE2=EF●EG
解析:略

练习册系列答案
相关题目
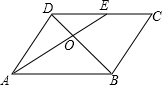 如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于( )cm2.
如图,在?ABCD中,E为CD中点,AE与BD相交于点O,S△DOE=12cm2,则S△AOB等于( )cm2.| A、24 | B、36 | C、48 | D、144 |
 14、如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为
14、如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为 如图,在?ABCD中,E为CD的中点,AE交BD于点F,则△EFD和△AFB的面积比为
如图,在?ABCD中,E为CD的中点,AE交BD于点F,则△EFD和△AFB的面积比为 如图,在?ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O.
如图,在?ABCD中,BD为对角线,EF垂直平分BD分别交AD、BC的于点E、F,交BD于点O.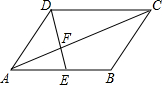 如图,在?ABCD中,E为AB的中点,DE交AC于F,△AEF∽
如图,在?ABCD中,E为AB的中点,DE交AC于F,△AEF∽