Question

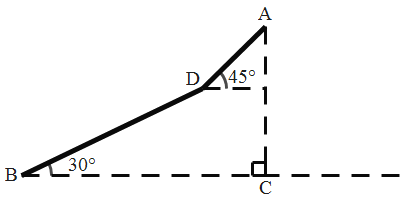
【题目】某地为打造宜游环境，对旅游道路进行改造．如图是风景秀美的观景山，从山脚B到山腰D沿斜坡已建成步行道，为方便游客登顶观景，欲从D到A修建电动扶梯，经测量，山高AC＝308米，步行道BD＝336米，∠DBC＝30°，在D处测得山顶A的仰角为45°，求电动扶梯DA的长.（结果保留根号）

Answer 1

【答案】140米

【解析】

作DE⊥BC于E，根据矩形的性质得到FC＝DE，DF＝EC，根据直角三角形的性质求出FC，得到AF的长，根据正弦的定义计算即可．

作DE⊥BC于E，

则四边形DECF为矩形，

∴FC＝DE，DF＝EC，

在Rt△DBE中，∠DBC＝30°，

∴DE＝BD＝168，

∴FC＝DE＝168，

∴AF＝AC﹣FC＝308﹣168＝140，

在Rt△ADF中，∠ADF＝45°，

∴AD＝AF＝140（米），

答：电动扶梯DA的长为140米．