Question

【题目】如图，点P是线段AB上的一个点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上，点M，N分别是对角线AC，BE的中点，连接MN，PM，PN，若∠DAP＝60°，AP2+3PB2＝2，则线段MN的长为_____．

Answer 1

【答案】

【解析】

连接PM、PN，△MPN是直角三角形，由勾股定理可得MN2＝PM2+PN2，在在Rt△APM中，AP＝2PM，在Rt△PNB中，PB＝PN，代入已知的AP2+3PB2＝2，即可．

连接PM、PN．

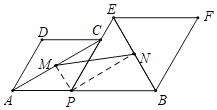
∵菱形APCD和菱形PBFE，∠DAP＝60°，M，N分别是对角线AC，BE的中点，

∴PM⊥AC，PN⊥BE，∠CAB＝∠NPB＝30°．

∴∠MPC+∠NPC＝90°，即△MPN是直角三角形．

在Rt△APM中，AP＝2PM，

在Rt△PNB中，PB＝PN．

∵AP2+3PB2＝1，

∴（2PM）2+3（PN）2＝2，

整理得PM2+PN2＝

在Rt△MPN中，MN2＝PM2+PN2，

所以MN＝．

故答案为：．